Hallo,
zunächst eine Warnung: dieser Beitrag ist relativ schwierig und ohne Vorkenntnisse in theoretischer Informatik nicht zu verstehen.
Im Laufe einer Lehrveranstaltung hat sich die Frage gestellt, ob die Primfaktorzerlegung (genauer: RSA – also 2 Primfaktoren) in NP liegt bzw. sogar NP-vollständig ist – ums populärer auszudrücken: wie viel Ärger bekommen wir, falls P=NP gilt.
Wir haben allerdings an dieser Stelle jedoch das Problem, dass die Komplexitätsklasse NP bzw. die Laufzeitfunktion NTIME auf Sprachprobleme – also Entscheidungen definiert ist. Innerhalb der Literatur finden sich wenig und vor allem sehr oberflächliche Aussagen darüber („es ist leicht einzusehen dass dieses Problem in NP liegt…“). Die letzten Wochen habe ich intensiver darüber nachgedacht und ich denke, eine brauchbare Lösung anbieten zu können.
Zunächst wichtige Vorarbeit: die Frage, ob eine natürliche Zahl eine Primzahl ist oder nicht, liegt in P (also deterministischer Polynomialzeit). Erreicht wird dies durch den AKS-Primzahltest. Damit ist auch die Frage, ob eine Zahl n (ungleich 1) Primteiler besitzt in P feststellbar, da dies immer der Fall ist, sofern es sich um keine Primzahl handelt (Hauptsatz der Zahlentheorie).
Im nächsten Schritt prüfen wir, ob die Zerlegung des RSA-Moduls in NP liegt.
 Nehmen wir hierzu beispielhaft die Primzahlen p=7 und q=11 also M=p*q = 7*11=77, binär dargestellt 1001101. Mittels eines naiven Nichtdeterministischen Algorithmus, können wir von 1 bis sqrt(M) alle möglichen Teiler durchprobieren. Dass dies in NP liegt, soll mittels der Abbildung gezeigt werden. Die Baumtiefe entspricht n/2, also die halbe Eingabelänge n(=7). Der Übersicht halber hier nur die Tiefe 3 anstelle 4.
Nehmen wir hierzu beispielhaft die Primzahlen p=7 und q=11 also M=p*q = 7*11=77, binär dargestellt 1001101. Mittels eines naiven Nichtdeterministischen Algorithmus, können wir von 1 bis sqrt(M) alle möglichen Teiler durchprobieren. Dass dies in NP liegt, soll mittels der Abbildung gezeigt werden. Die Baumtiefe entspricht n/2, also die halbe Eingabelänge n(=7). Der Übersicht halber hier nur die Tiefe 3 anstelle 4.
Durch diese Verzweigung erhalten wir also alle Lösungskandidaten h.
Im blauen Kasten prüfen wir nun, ob h ein Primteiler von M ist. Sowohl der Primzahltest „ist h eine Primzahl?“ liegt in P (wie oben erwähnt), als auch die Division „ist h ein Teiler von M“. Auch würde der Primzahltest des zweiten Divisors in P liegen. Dementsprechend liefert der skizzierte Nichtdeterministische Algorithmus am Ende ein „ja“, da 111 (=7) sowohl Primzahl, als auch Teiler von M (77) ist.
Wir haben also nun festgestellt, dass die Frage nach der Primfaktorzerlegung in NP liegt. Das hilft uns allerdings nur bedingt, da diese Antwort schon vorher bekannt war. Per Definition besitzt ein RSA-Modul zwei Primteiler, daher würde der Algorithmus natürlich stets ein ja liefern. Wir müssen also dieses Entscheidungsproblem (1) nutzen, um effizient das Optimierungsproblem (2) zu lösen.
Aus diesem Grund definieren also das Problem in folgender Weise neu:
Eingabe: (M,k) wobei m das RSA-Modul (bestehen aus dem Produkt zweier Primzahlen), und k eine beliebige Zahl k<=M.
Zulässige Lösung: ja/nein
Frage: liegt ein Primfaktor des RSA-Moduls M unterhalb von k.
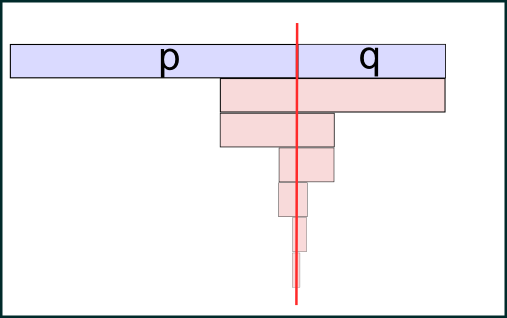
Wir übergeben also das Modul M=(p*q) und fragen, ob sich der kleinere Primfaktor unterhalb von k befindet. Dieses Entscheidungsproblem ändert am oben skizzierten Algorithmus die Laufzeit nur um einen konstanten Faktor, welche in der polynomiellen Unschärfe sowieso verschwindet. Wir sind inder Lage, wie in der nächsten Abbildung zu sehen, mittels einer binären Suche den Primfaktor exakt zu bestimmen:
Können wir also das Entscheidungsproblem (1) als Orakel verwenden, so lässt sich auch dieses Optimierungsproblem (2) sehr effizient (logarithmisch) lösen. Die binäre Suche geht in der polynomiellen Unschärfe verloren, womit wir informell bewiesen haben: bei P=NP liegt die Faktorisierung auch in P.
Welche Auswirkungen hätte P=NP auf den Alltag? Diese Frage lässt sich leider nicht beantworten, da nicht jeder Algorithmus in P auch effizient ist. Wäre der Exponent jedoch niedrig, wären die Folgen schwerwiegend: die PKI würde zusammenbrechen, wodurch sicheres Online Banking unmöglich wäre. Jedes asymmetrische und damit auch jedes hybride Verschlüsselungssystem wäre hinfällig. Die Quantenkryptographie, die hiervon nicht betroffen wäre, liefert keinen adäquaten Ersatz.
Hoffen wir also, dass P != NP gilt.

Schreibe einen Kommentar zu mtkwschneyder@yahoo.com Antworten abbrechen