In einem Beitrag habe ich eine vereinfachten Variante von Kyber auf Basis von LWE (Learning With Errors) erläutert. In diesem Fall sind die Koeffizienten der Matrizen und Vektoren ganze Zahlen. Dies genügte, um den groben Ablauf und die Falltür zu verstehen. Es entspricht damit jedoch nicht mehr ganz dem Original. Beim „echten“ Kyber sind die Vektor- und Matrixkomponenten nämlich Polynome aus einem Polynomring.

Um dem nachvollziehbaren Anspruch an Korrektheit zu genügen, möchte ich an dieser Stelle nun Kyber auf Basis von „Module Learning with Errors“ näher erläutern. Im ersten Teil werden hierzu die erforderlichen Operationen, also Addition und Multiplikation in einem Polynomring, näher definiert. Im zweiten Teil werden dann schrittweise die Ver- und Entschlüsselungsschritte betrachtet. Den Abschluss bildet die Korrektheitsbetrachtung.

Hinweis: Einige Teile wurd aus dem Originalbeitrag entnommen, sofern dies sinnvoll erschien.

Operationen

In Kyber werden die grundlegenden Operationen auf Basis von Polynomen durchgeführt. Egal ob Skalar, Matrix oder Vektor: jede Komponente besteht aus einem Polynom. Ein solches Polynom könnte beispielsweise so aussehen:

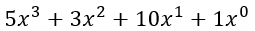
Um den Darstellungsaufwand etwas zu verringern, können wir dies auch als Tabelle darstellen:

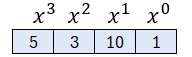
Und da die Potenzen in der Überschrift immer von rechts nach links aufsteigend stets identisch sind, können wir dies weiter zu einer Liste/4-Tupel vereinfachen:

Bevor wir die Addition zweier Polynome betrachten, müssen wir noch festhalten, dass in Kyber alle Operationen Modulo einer Primzahl p durchgeführt werden. Dies ist daher ganz analog zur vereinfachten Variante, wo wir ebenfalls alle Werte Modulo p reduziert haben. Dies betrifft auch alle Koeffizienten der Polynome: Weist also ein Koeffizient einen Wert >=p auf, können wir unmittelbar Modulo p rechnen. Hier und im Folgenden soll p=17 gelten. Jede Summe und jedes Produkt wird daher Modulo 17 gerechnet.

Schauen wir uns die Addition an. Hierbei werden die Koeffizienten miteinander addiert, wie man es auch ohne Kenntnis um Polynome erwarten würde. Das Ergebnis wird im Anschluss modulo p also modulo 17 reduziert. Somit erhalten wir Koeffizienten aus dem Intervall [0,p[.

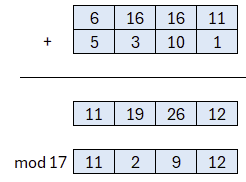
Zum besseren Verständnis noch ein weiteres Berechnungsbeispiel:

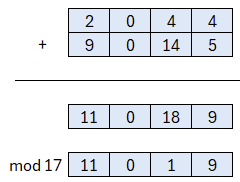
Etwas schwieriger als die Addition gestaltet sich hingegen die Multiplikation. Der Anfang ist dabei sehr ähnlich einer Schulbuch-Multiplikation und leicht verständlich. Allerdings muss sichergestellt sein, dass die Polynome nicht länger werden, denn alle Polynome in Kyber haben eine feste Länge. In unserem Beispiel ist der Grad 3 weshalb wir von 0-3 insgesamt 4 Koeffizienten haben. Im „echten“ Kyber ist der Grad 255 weshalb wir mit 256 Koeffizienten umgehen müssen. Bekanntlich ist jedoch das Ergebnis einer Multiplikation, das Produkt, nicht selten eine deutlich größere Zahl als die ursprünglichen Faktoren. Aus diesem Grund wird zunächst eine Multiplikation durchgeführt und das Ergebnis anschließend mit einer Polynomdivision wieder verkleinert um auf die feste Länge von 4 (oder 256 in Kyber) zu kommen.

Zunächst starten wir mit der Multiplikation an einem einfachen Beispiel.

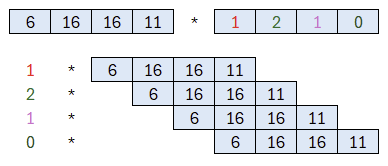
Wie erwähnt ähnelt der Start dem Schulbuchverfahren – wir führen die Multiplikation durch und betrachten das Ergebnis.

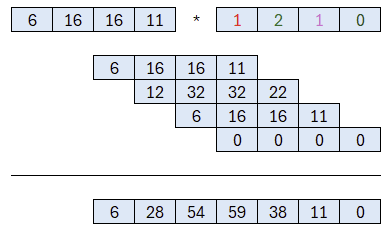
So wie bei der Addition müssen wir die Koeffizienten im Ergebnis modulo p reduzieren.

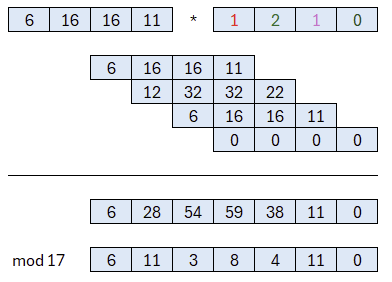
Und erhalten ein Polynom vom Grad 6. Nur damit wir nicht vergessen, dass es sich um Polynome handelt, möchte ich das Ergebnis nochmal in dieser Form präsentieren:

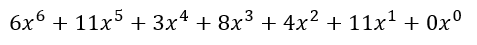
Dieses Produkt, als Ergebnis der Multiplikation zweier Polynome vom Grad 3 (und somit der Grad 6) ist jedoch zu lange. In Kyber haben alle Polynome dieselbe Länge. Aus diesem Grund müssen wir das Ergebnis mittels Polynomdivision verkleinern. Hierfür wird ein irreduzibles Polynom verwendet. Das ist in Kyber 2²⁵⁶+1. Hier, in unserem Beispiel, verwenden wir b=2⁵+1. Irreduzible Polynome werden Informierte bereits aus den Galois-Feldern kennen, wie sie bei der S-BOX von AES und im GCM-Betriebsmodus zum Einsatz kommen. Falls nicht, ist das jedoch nicht weiter tragisch und so betrachten wir dieses Polynom als ein besonderes, welches wir zur Division nutzen.

Dieses Polynom b ist mit Absicht nicht blau eingefärbt, um ihn von den anderen Polynomen besser unterscheiden zu können. Alle Multiplikationen werden daher durch dieses Polynom dividiert. Das Ergebnis ist für uns nicht wichtig, sondern nur das, was übrig bleibt, ist von Interesse. Somit multiplizieren wie die Koeffizienten von b jeweils um einen Wert und subtrahieren dies von unserem Polynom. Der Wert ergibt sich aus dem höchstwertigen Koeffizienten. Am Ende muss das Ergebnis modulo p also modulo 17 reduziert werden.

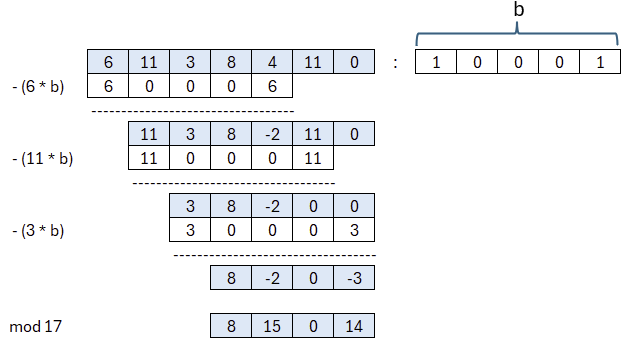
Das Ergebnis ist also:

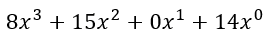
Zum besseren Verständnis noch ein weiteres Beispiel.

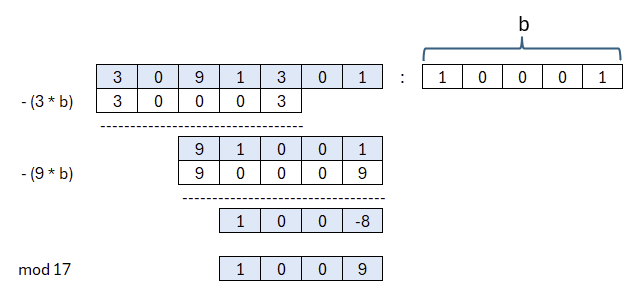
Auf diese Weise können wir alle Multiplikationsergebnisse wieder in die vierelementige Form bringen. Damit sind auch alle erforderlichen Operationen beschrieben. Sofern die Ausführungen für Addition und Multiplikation nachvollziehbar waren, sind damit nun alle wesentlichen Werkzeuge für Kyber bekannt.

Schlüsselgenerierung

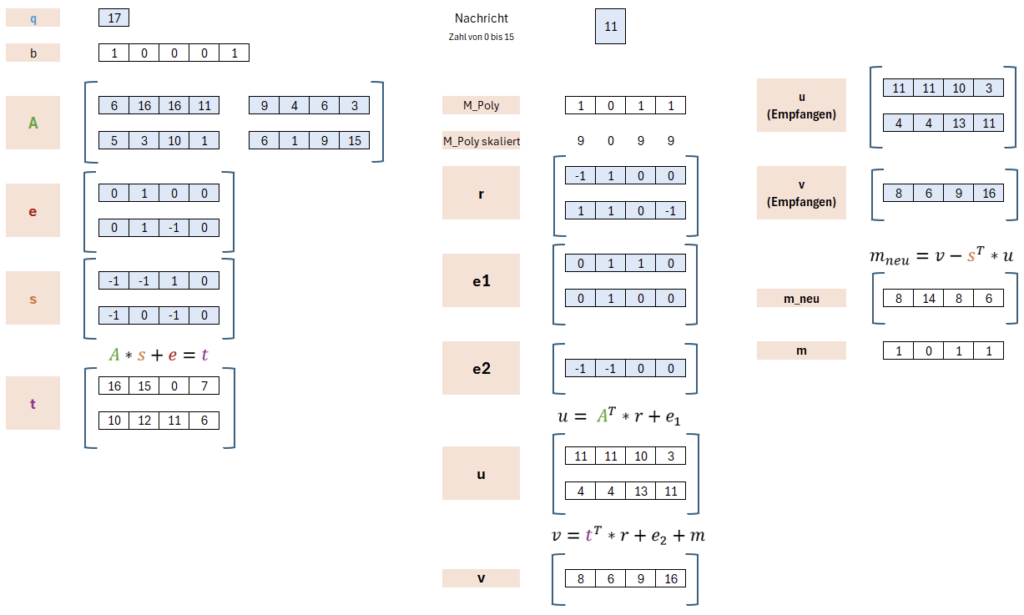
Der öffentliche Schlüssel besteht in Kyber aus einer Matrix A und einem Vektor t.

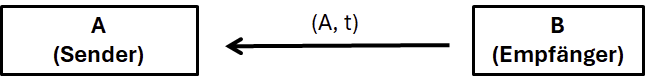
Hierbei muss jedoch berücksichtigt sein, dass es sich bei den Komponenten der Matrizen und Vektoren um Polynome handelt. Wir haben daher, in diesem Beispiel, eine 2×2-Matrix als A mit vier Polynomen und ein Vektor t mit zwei Polynomen. Wir wollen nun Schrittweise A und t bestimmen.

Betrachten wir zunächst die 2×2-Matrix A. In Kyber wird diese zufällig gewählt. Genaugenommen wird diese auch einem 256-Bit Random-Seed deterministisch berechnet. Auf diese Weise muss weniger Schlüsselmaterial übermittelt werden. In unserem Fall füllen wir einfach die Polynome mit zufälligen Koeffizienten kleiner p.

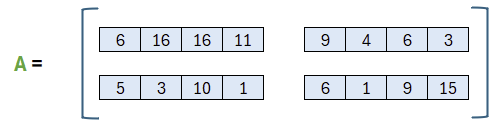
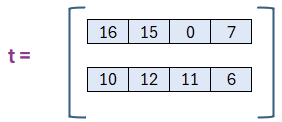
Damit haben wir A beschrieben (bzw. zufällig gewählt). Der Vektor t ermittelt sich aus einem Produkt von A mit s und einer Addition mit e. Schauen wir uns deshalb zunächst s und e an bevor wir daraus t ermitteln.

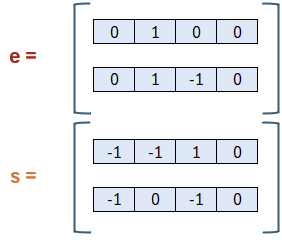
Die Vektoren e und s können, so wie die Matrix A, beliebig gewählt werden. Für e ist wichtig, dass nur kleine Koeffizienten (nahe der 0) gewählt werden. Bei s ist dies nicht ganz so wichtig, dennoch wird das Verfahren nicht unsicherer, wenn wir es hier gleichtun. Daher wurden hier Werte nahe der 0 gewählt. Genaugenommen handelt es sich bei -1 um 18, da -1 modulo 19 = 18 ist. Allerdings wird durch die Verwendung von -1 deutlicher, dass Koeffizienten nahe der 0 sind. Aus diesen Koeffizienten bestimmt sich nun t:

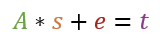
Es findet somit eine Multiplikation von A mit s statt wobei e auf das Ergebnis addiert wird. Alle Ergebnisse können stets modulo q (also modulo 19) reduziert werden.

Die Multiplikation Matrix mit Vektor wird exakt so ausgeführt, wie es aus der linearen Algebra bekannt ist. Nur werden für die Multiplikation und Addition die oben definierten Operationen angewendet.

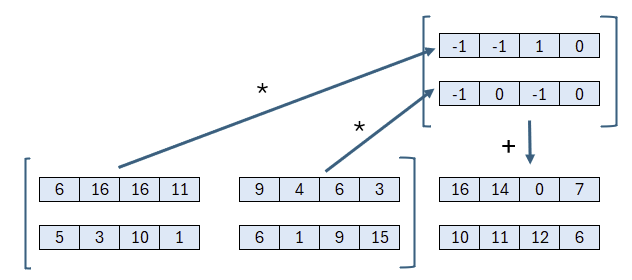
Für die erste Komponente des Ergebnisvektors wird somit berechnet:

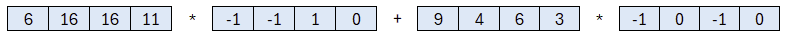
Wer sich fragt, wie das Ergebnis zustande kommt, kann sich die zwei Multiplikationen und die Addition nun genauer ansehen.

Erste Multiplikation mit Polynomdivision

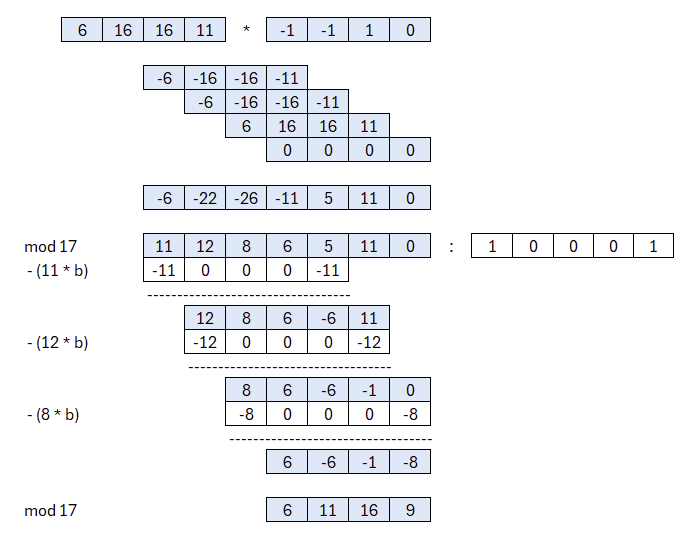
Zweite Multiplikation mit Polynomdivision

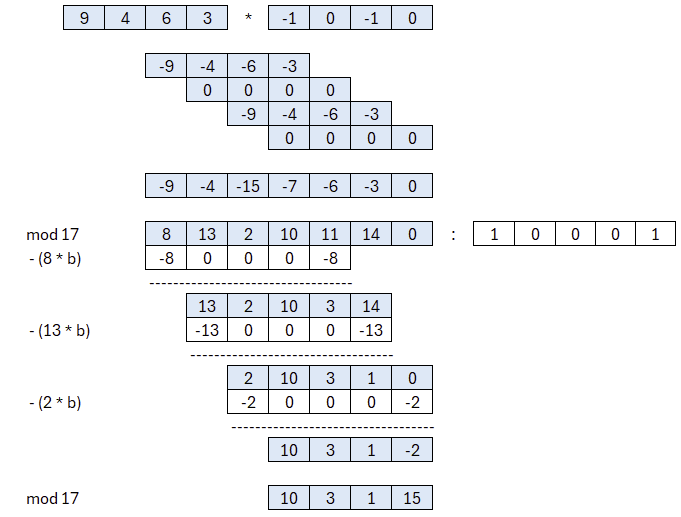
Addition

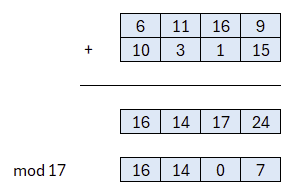
Auf diese Weise berechnet sich der Ergebnisvektor A * s. Um fortzufahren, wird das Ergebnis mit e, dem Fehler, addiert:

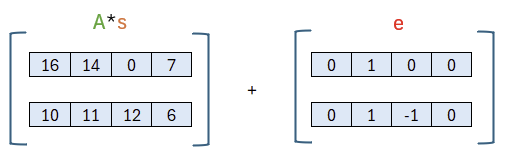
Und erhalten so die zweite Komponente für unseren öffentlichen Schlüssel.

An dieser Stelle lohnt es sich vermutlich kurz zu rekapitulieren was hier gemacht wurde. Eine zufällig bestimmte aber öffentlich bekannte Matrix A wurde mit einem Vektor s multipliziert und im Anschluss das Ergebnis mit einem Vektor e addiert. Bei s handelt es sich um den privaten Schlüssel. Würde man lediglich das Produkt aus A und s bilden, könnte die Operation mit dem Gauß-Algorithmus umgekehrt werden. Allerdings haben wir auch ein Fehlervektor e, welcher im Anschluss hinzugegeben wurde. Somit wäre die Suche nach dem privaten Schlüssel eine Umkehrung unter Berücksichtigung zufälliger Fehlervektoren. Es wird angenommen, dass dies auch für Quantencomputer nur schwer durchführbar ist.

Wir haben nun unseren öffentlichen Schlüssel erzeugt. Dieser besteht aus der Matrix A und dem Vektor t und kann dem Sender übermittelt werden. In unserem Fall ist der Sender die Person, die gerne eine Nachricht übermitteln möchte, und der Empfänger soll diese im Anschluss entschlüsseln. Somit hat der Empfänger das Schlüsselmaterial generiert und übermittelt dies dem Sender.

Verschlüsselung

Wir haben nun erfolgreich Schlüsselmaterial erzeugt. Der Sender, der eine Nachricht verschlüsseln möchte, wird nun im Folgenden zwei Komponenten erzeugen: u und v. Wir wissen noch nicht, wie diese aussehen. Aber vermutlich lässt sich schon erahnen, dass eine dieser Komponenten die Nachricht m enthalten wird. Spoileralarm: In v ist die verschlüsselte Nachricht enthalten und u wird benötigt um diese, mit Kenntnis des privaten Schlüssels s, beim Empfänger auszupacken.

Bevor wir uns mit u und v befassen, müssen wir zunächst über die Nachricht m sprechen. Unsere Nachricht m besteht aus den Bits 0 und 1. Möchten wir beispielsweise die Bits 1011 übermitteln, können wir diese als Polynom darstellen:

Um in Kyber eine Nachricht zu übermitteln, muss diese vorher skaliert werden. Skalieren bedeutet, mit p/2 (also 17/2) zu multiplizieren und im Anschluss aufzurunden. In unserem Fall machen wir hierzu aus jeder 1 eine 9 und die Nullen lassen wir stehen.

Dies ist unsere um (p/2)-skalierte Nachricht m. Wenn im Folgenden von m, also der Nachricht, die Rede ist, ist damit diese skalierte Folge gemeint. Die Skalierung wird notwendig werden, da die Entschlüsselung nicht verlustfrei ist. Nach der Entschlüsselung sind die Werte nicht mehr, so wie hier 9099 sondern können leicht davon abweichen, z.B. 8179. In diesem Fall lässt sich jedoch recht leicht die vorherige Folge 9099 wiederherstellen, da jede 7 oder 8 näher an der 9 ist und jede -1, 0, 1 näher an der 0.

Wir definieren also die Nachricht m als die skalierte Nachricht.

Zur weiteren Verschlüsselung werden ein Vektor r, ein Vektor e₁ und ein Skalar e₂ mit zufälligen Werten benötigt, allerdings: Wie oben bei e und s sollen es kleine Koeffizienten sein, also in diesem Beispiel mit 1, 2 oder 3. An dieser Stelle nochmal ganz deutlich: Das sind zufällig gewählte Werte, wir können diese auch unbeschadet anders wählen!

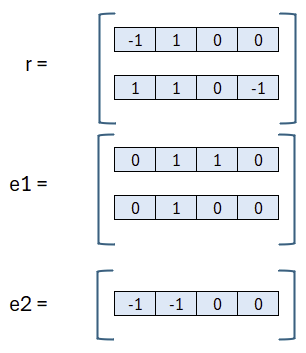
Nun sind wir bereit, um uns u und v genauer anzusehen. Beginnen wir mit u.

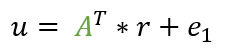
Das „^T“ im Exponenten beschreibt hier die transponierte Matrix. Transponieren bedeutet, dass wir die Matrix einmal an der Hauptdiagonalen spiegeln: Aus Zeilen werden Spalten und umgekehrt. Schauen wir uns das an:

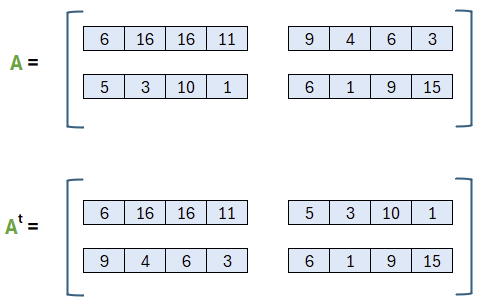
Die Hauptdiagonale bleibt unverändert und es tauschen nur zwei Polynome. Im nächsten Schritt können wir durch eine Multiplikation und eine Addition (stets modulo q) das u ermitteln.

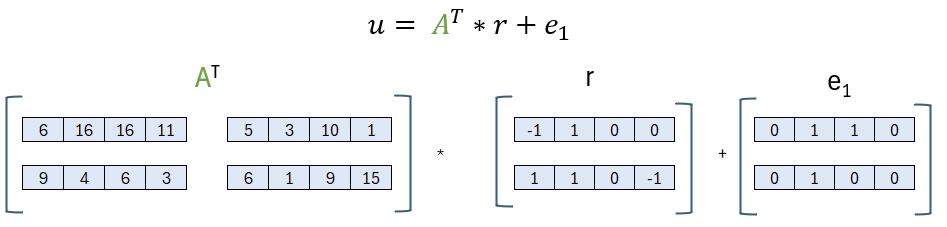
Um u zu berechnen, müssen wir also die bereits bekannte Matrix A transponieren und mit dem Zufallsvektor r multiplizieren und e₁ addieren. Falls es nicht direkt bemerkt wurde: bei u kommt wieder unsere Falltür ins Spiel, nur mit neuen Werten. Die Falltür wurde also sowohl zur Generierung des öffentlichen Schlüssels benutzt als auch hier zur Verschlüsselung.

Jetzt schauen wir uns die zweite Komponente, also das v näher an:

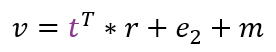
In diesem Fall wird nicht eine Matrix transponiert, sondern ein Vektor. Zuvor hatte t zwei Zeilen und eine Spalte. Nach der Transposition hat t somit eine Zeile und zwei Spalten. Auf diese Weise ist somit auch die Skalarmultiplikation mit r definiert: das Ergebnis ist jedoch, wie immer, ein Polynom. Abschließend werden e2 und m addiert.

Wir haben nun erfolgreich unsere Nachricht m=1011 verschlüsselt und erhalten zur verschlüsselten Übermittlung der Nachricht die 6. Zur Entschlüsselung ist natürlich beides erforderlich: das u und das v.

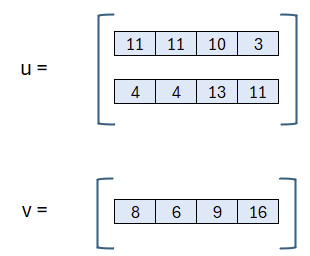
Die Werte können nun dem Empfänger übermittelt werden.

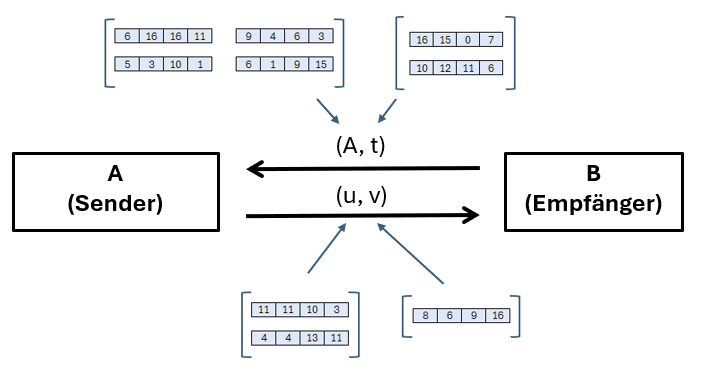
Sind u und v erfolgreich beim Empfänger angekommen, können wir nun mit der Entschlüsselung der Nachricht starten.

Entschlüsselung

Denn während die Verschlüsselung etwas Arbeit ist, gestaltet sich die Entschlüsselung doch recht einfach. Dabei ist m_neu das Ergebnis der Entschlüsselung. Später wird noch deutlich, weshalb dort m_neu und nicht nur m steht.

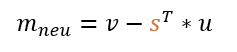
Wir transponieren also unseren geheimen Schlüssel s und multiplizieren dies mit dem vom Sender empfangenen Vektor u und ziehen das Ergebnis von v ab.

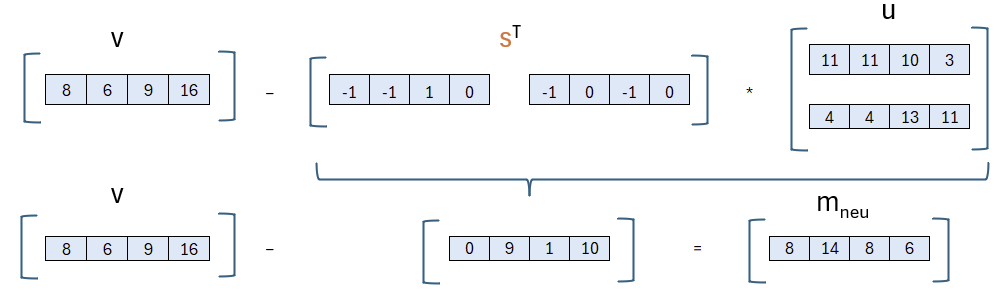
Nur wenn wir s transponieren, bekommen wir das Produkt der Polynome errechnet. Aber… machen wir damit nicht einiges kaputt, wenn wir das einfach transponieren? Nein, denn in v steckt ja auch das transponierte t und im transponierten t steckt impliziert auch das (dann transponierte) s. Das wird im Abschnitt zur Korrektheit noch genaure erläutert.

Wir haben nun erfolgreich die übermittelte Nachricht entschlüsselt.

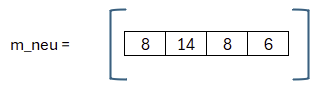
Aber… was ist denn das? Das m_neu=8 14 8 6 weicht ja von der ursprünglichen Nachricht m=1 0 1 1 ab? Alles falsch? Nein! Das ist richtig und erwartet. Immerhin haben wir mit r, e, e₁ und e₂ mehrere „Fehler“ in der Berechnung, die am Ende nicht alle wieder entfernt werden können. Wir haben für diese Fehler jedoch stets kleine Koeffizienten gewählt. Daher ist hier die Erwartung, dass sich das Ergebnis auch nur leicht verschiebt. Bei Kyber kommen wir deshalb nicht exakt auf den ursprünglich verwendeten Wert. Aber dadurch, dass es eine „kleine“ oder eine „große“ Zahl ist, können wir das ursprüngliche Bit wiederherstellen.

Wenn wir die Werte 8, 14, 8 und 6 danach bewerten, wie weit die Werte von der 0 oder der 9 entfernt sind, kommen wir zu dem Schluss, dass 8 vermutlich eine 9 war, dass 14 vermutlich die 0 war und 6 ebenfalls recht nahe an der 9 ist. Tatsächlich ist dies bei der kleinen Primzahl p (hier 17) alles recht knapp. Im Original wird eine größere Primzahl verwendet (p=3329) weshalb das Ergebnis eindeutiger sein sollte. Allerdings: Auch im Original kann eine Entschlüsselung aus ungünstigen e,s,e1,e2-Werten fehlschlagen. Das wird im Protokoll jedoch berücksichtigt.

Korrektheit

Der beste Weg die Korrektheit des Verfahrens nachzuvollziehen zu können, ist am Ende anzufangen und rückwärts die Variablen zu substituieren. Wir starten daher bei der Entschlüsselung und ersetzen jeweils u und v durch die vorherigen Berechnungen.

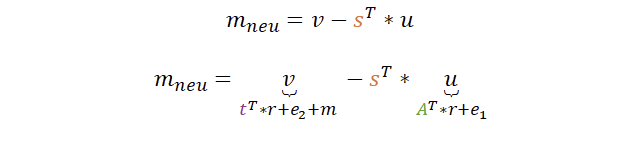
Wir sind noch nicht ganz fertig, denn auch das t (welches in u enthalten ist) haben wir ganz am Anfang aus A, s und e berechnet:

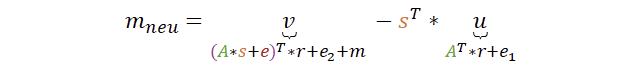
Wir ersetzen nun entgültig v und u und schauen uns das Ergebnis an, ohne dabei den Überblick zu verlieren.

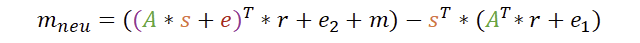
Nun stellt sich die Frage, was man hier alles vereinfachen kann. Zum einen kann man sich die Rechengesetze zur transponierten Matrix ansehen. Ich fasse es kurz zusammen:

• (A + B)^T = A^T + B^T
• (A * B)^T = B^T * A^T

Auf dieser Basis können wir die erste Klammer, das ursprüngliche t, ganz einfach umwandeln:

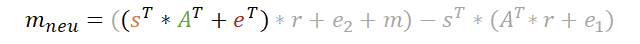
Zum anderen können wir diese Klammer mit dem r ausmultiplizieren, welches unmittelbar daneben steht.

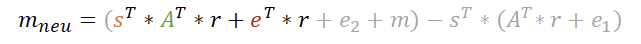
Jetzt schauen wir uns mal die rechte Seite an. Bitte daran denken das Vorzeichen vor dem s zu berücksichtigen!

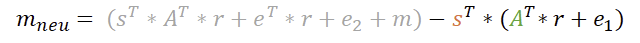
Also multiplizieren wir die rechte Seite aus wie bekannt.

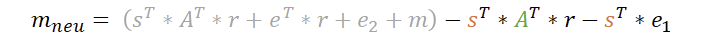
Da wir jetzt fertig sind, können wir alle Klammern entfernen und uns das Ergebnis anschauen.

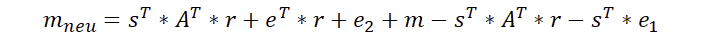
Eine ganze Menge Zeug. Aber wie in der Schule schaut man einfach, ob ein Produkt doppelt mit unterschiedlichem Vorzeichen vorkommt. Das ist glücklicherweise der Fall!

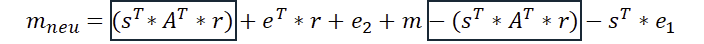
So können wir erkennen, dass wir die Matrix A vollständig entfernt bekommen. Aber es wird auch sichtbar, dass einiges übrig bleibt. Wir können mal überlegen, ob wir hier noch etwas verbessern können.

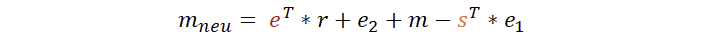
Zur Erinnerung: e hat zwar der Empfänger gewählt, aber das r stammt vom Sender. Das e₂ stammt auch vom Sender und können wir als Empfänger nicht entfernen. Zwar kennen wir als Empfänger den privaten Schlüssel s, jedoch stammt e₁ vom Sender und ist daher unbekannt. An den Farben lässt sich leicht erkennen, dass wir hier als Empfänger nichts mehr tun können. Daher sind wir hier fertig.

An dieser Stelle sollte klar werden, warum die Koeffizienten für die Fehler e, e₁, e₂ und r klein gewählt wurden. Sie verbleiben nach der Verschlüsselung noch im Ergebnis und können nicht restlos entfernt werden. Im Extremfall kann dies tatsächlich dazu führen, dass die Nachricht nicht korrekt entschlüsselt werden kann. Das wurde jedoch im Verfahren bereits berücksichtigt, sollte aber nur selten eintreten.

Weitere Informationen

Sehr interessant ist der Baby Kyber von Ruben Gonzalez, in dem auch genauer auf die Berechnungen im Polynomring eingegangen wird; die Zahlen aus seinem Beispiel wurden auch hier verwendet. Natürlich weise ich auch gerne auf das Originalpapier hin.

Abschließend möchte ich an dieser Stelle noch die Kyber-Implementierung in Excel zur Verfügung stellen. In diesem Dokument kann das oben dargestellte Beispiel vollständig nachvollzogen werden.

Auf Makros wurde verzichtet; aufgrund der Lambda-Funktionen wird das Ergebnis jedoch nur unter Office 365 oder Excel 2024 lauffähig sein.

_{SHA256: C461EA5C1C0564A96350B9F766F4EE3AC6CCCD612D481801E35E5924E354D130}