Das hier dargestellte mehrschichtige neuronale Netz mit 3 Eingabeneuronen plus Bias, 3 Hidden-Neuronen plus Bias und einem Outputneuron ist ein grundlegendes Beispiel für künstliche neuronale Netze, welches zur Mustererkennung oder für einfache Klassifikationsaufgaben verwendet werden kann.
In diesem bereitgestellten Excel-Dokument können die Verarbeitungsschritte näher betrachtet werden.
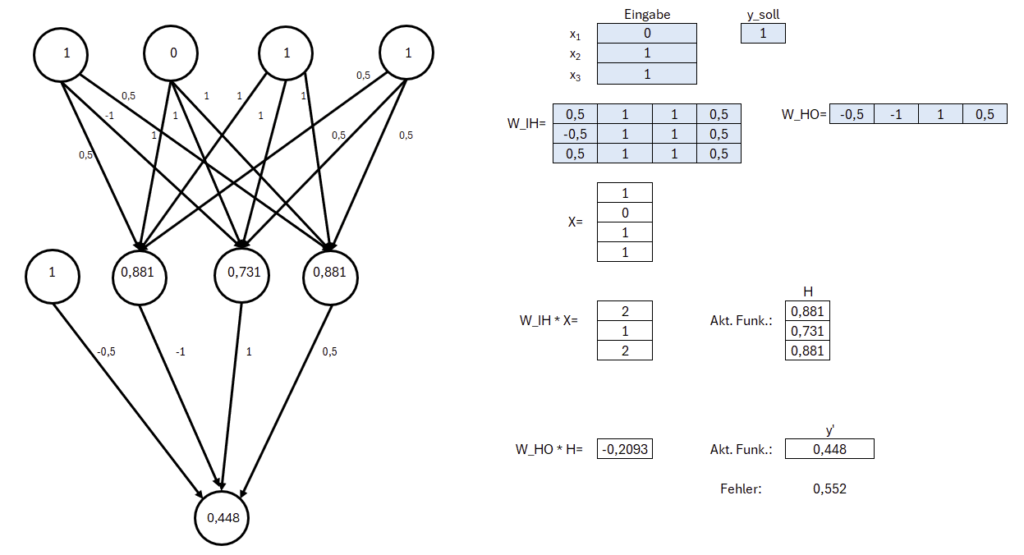
In diesem Beispiel dienen drei Eingabeneuronen dazu, die Merkmale oder Attribute der Eingabedaten aufzunehmen; z. B. eine einfache logische Verknüpfung wie ein XOR. Der Bias ist ein zusätzliches Neuron, das stets den Wert 1 hat. Er ermöglicht es dem Netzwerk, die Aktivierungsfunktion nach oben oder unten zu verschieben, was die Flexibilität beim Lernen erhöht. Die Hidden-Schicht besteht hierbei aus drei Neuronen. Jedes Hidden-Neuron erhält Eingaben von allen Neuronen der vorherigen Schicht (inklusive des Bias). Diese Eingaben werden mit bestimmten Gewichten multipliziert und summiert. Auf diese gewichtete Summe wird dann eine Aktivierungsfunktion angewendet, wie zum Beispiel die Sigmoid-Funktion. Diese Funktion führt Nichtlinearitäten ein, wodurch das Netzwerk komplexere Muster erlernen kann. Das Outputneuron erhält die Ausgaben der Hidden-Neuronen (wiederum multipliziert mit entsprechenden Gewichten) und summiert sie. Nach Anwendung der Aktivierungsfunktion liefert es die finale Ausgabe des Netzwerks. Diese Ausgabe könnte beispielsweise die Wahrscheinlichkeit darstellen, dass ein bestimmtes Ereignis eintritt, oder eine Klassenzugehörigkeit in einem Klassifikationsproblem.
Im ersten Tabellenblatt „(1) Vorwärts“ werden die Berechnungsschritte dargestellt, mit denen das neuronale Netz zu einem Ergebnis kommt. Hierbei ist leicht einzusehen, dass die Ausgabe 0.448 von der erwarteten Ausgabe 1 abweicht.
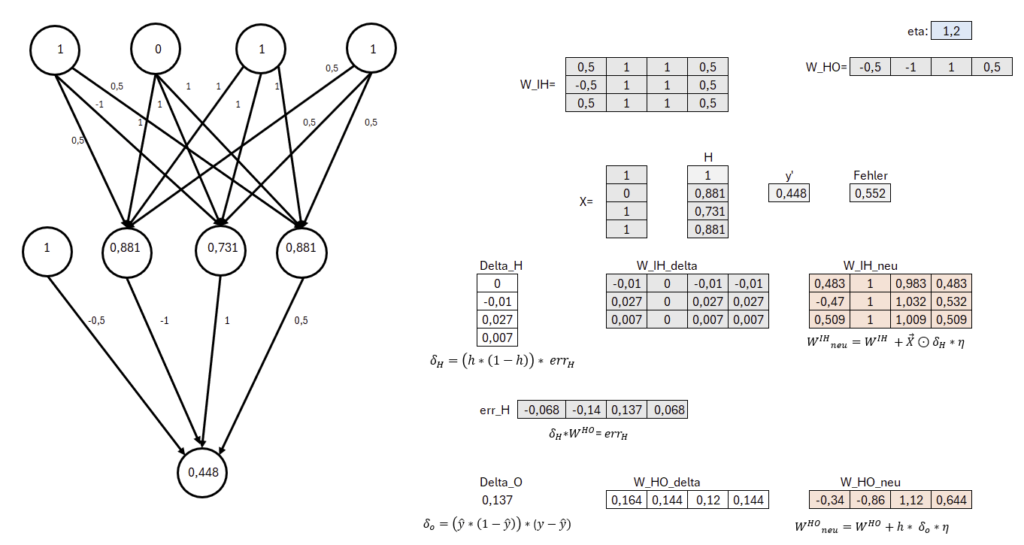
Um das Netzwerk zu trainieren, wird ein Lernalgorithmus wie der Gradientenabstiegsverfahren verwendet kombiniert mit Backpropagation. Dabei werden die Gewichte im Netzwerk iterativ angepasst, um den Fehler zwischen der vorhergesagten Ausgabe und der tatsächlichen Zielausgabe zu minimieren. Der Fehler wird dabei rückwärts durch das Netzwerk propagiert, und die Gewichte werden in Richtung des steilsten Abstiegs im Fehlerraum aktualisiert. Die Berechnungsschritte der Backpropagation werden auf dem zweiten Tabellenblatt „(2) Rückwärts“ dargestellt. Somit ist das Ergebnis des zweiten Berechnungsschrittes eine neue Gewichtungsmatrix, die für eine erneute Vorwärtsberechnung dienen kann.
Dieser Vorgang muss über mehrere Runden (Iterationen) ausgeführt werden, damit die Gewichte entsprechend der gewünschten Funktion angepasst werden. Aus diesem Grund wird auf dem 3. Tabellenblatt „(3) Mehrfach“ der Vorgang 4000 Iterationen mit verschiedenen Eingaben wiederholt.
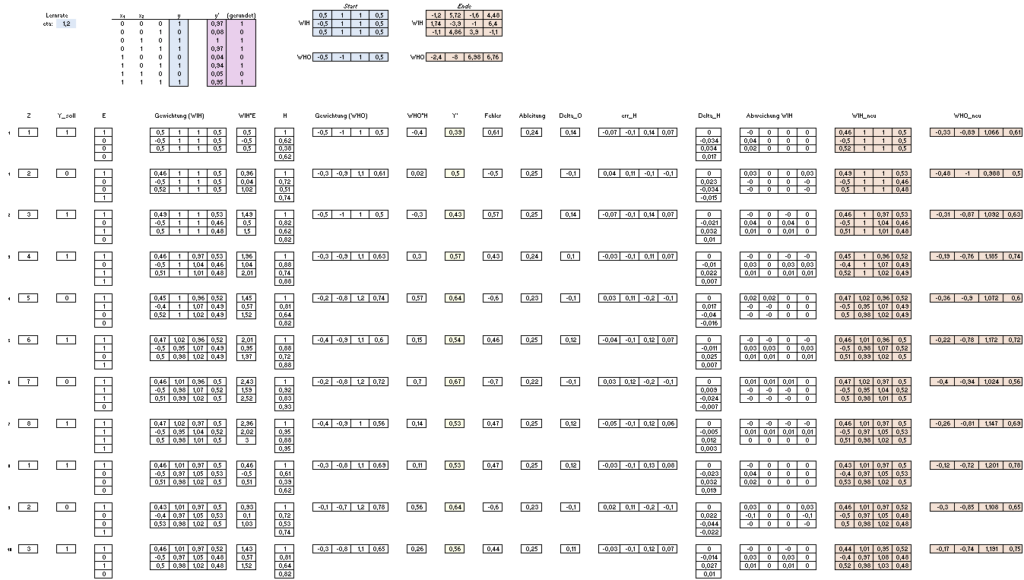
Auf dem dritten Tabellenblatt kann ferner festgelegt werden, welche Funktion antrainiert werden soll. Hierbei ist eine Funktion voreingestellt, kann jedoch leicht über die Wertetabelle (in blau) geändert werden, um eine andere dreistellige Funktion zu trainieren.
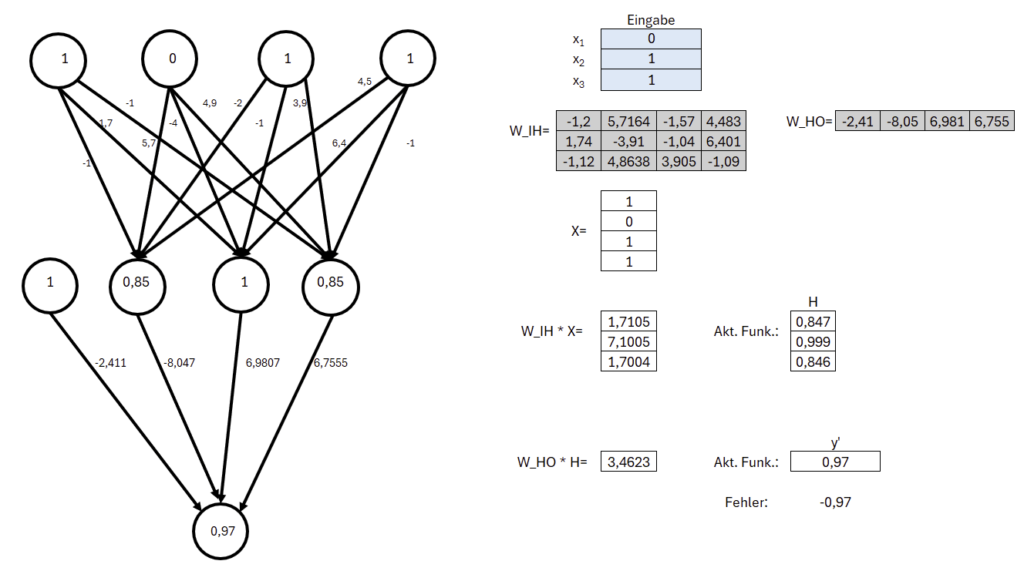
Im vierten Tabellenblatt „(4) Vorwärts neu“ kann auf Basis der neu kalkulierten Gewichtung über die Eingabemöglichkeit nachvollzogen werden. Die Gewichtungen wurden von den vorherigen Iterationen übernommen.
Download der Microsoft Excel-Datei. Auf den Einsatz von Makros wurde verzichtet.
SHA256: 5DC63414DAC1D5B2F273FE775D9DB0FF76C802BEE3744F4EE86F5DA673E51BA4
