In August 2025, NIST standardized a lightweight encryption algorithm. It was designed to run both securely and efficiently on resource-constrained devices. Examples include IoT sensors, embedded systems, or RFID chips. Alongside the encryption algorithm, a hash function and two XOF variants were also standardized.

Structure of the Cipher

The process begins with initialization: a 320-bit initial state is formed using a fixed IV, a key, and a nonce. Then the stronger permutation (12 rounds) is applied, which is explained in more detail below. The key is mixed in again at the end, ensuring that the initial state is unique.

Next, the associated data (AD) is processed. Each AD block is XORed into part of the state, followed by the lighter permutation rounds (8 rounds). Associated data provides a way to authenticate additional unencrypted plaintext through the tag. An example could be an IP address or another user identifier.

After that, the plaintext is encrypted. The first block is directly linked with the current state; the plaintext is XORed with it to produce the ciphertext. At the same time, the processed block is mixed back into the state, followed by 8 more permutation rounds if further blocks need to be encrypted.

Finally comes the finalization: the key is mixed into the state once again, 12 more permutation rounds are performed, and the authentication tag is extracted from the state. The result is: ciphertext + tag. The tag covers both AD and ciphertext, ensuring that any tampering is detected during decryption.

Core of the Cipher: Permutation Rounds

At the heart of Ascon are the 320-bit permutation rounds with five 64-bit words (denoted S[0] to S[4]). Each round has three steps: A round-specific constant is added into the state (AddConstant).

The substitution layer provides nonlinearity: the same 5-bit S-box is applied to every bit-column of the five words. This is illustrated in the figure below.

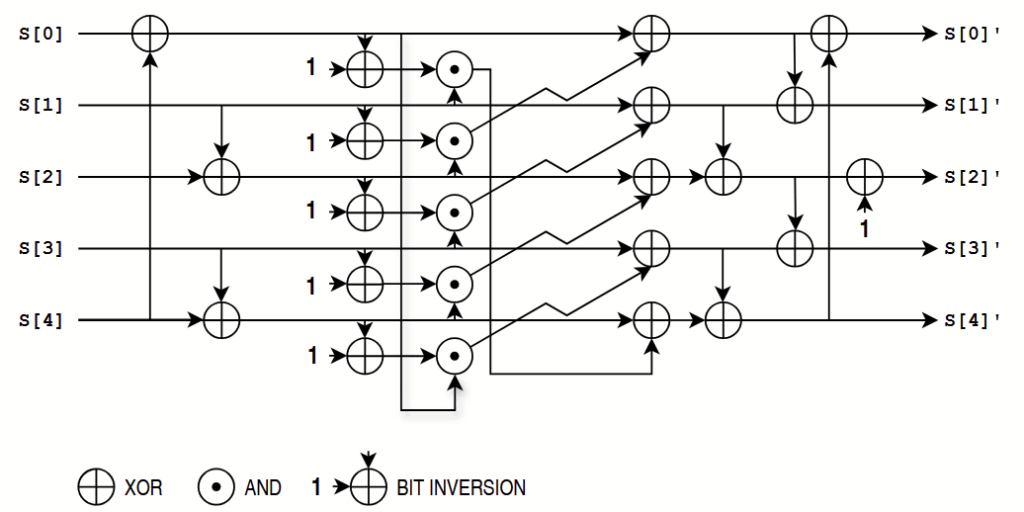
Finally, the linear diffusion spreads bit influence: each word is XORed with rotated copies of itself. The rotation offsets differ per word (e.g., 19/28, 61/39, etc.), ensuring that bit effects quickly diffuse across all words. This sequence is repeated multiple times to form the permutation.

\newcommand{\shiftr}[2]{#1 \mathbin{\ggg} #2} 

\begin{align}
S_0 &= S_0 \oplus (\shiftr{S_0}{19}) \oplus (\shiftr{S_0}{28}) \\
S_1 &= S_1 \oplus (\shiftr{S_1}{61}) \oplus (\shiftr{S_1}{39})\\
S_2 &= S_2 \oplus (\shiftr{S_2}{1}) \oplus (\shiftr{S_2}{6}) \\
S_3 &= S_3 \oplus (\shiftr{S_3}{10}) \oplus (\shiftr{S_3}{17})\\
S_4 &= S_4 \oplus (\shiftr{S_4}{7}) \oplus (\shiftr{S_4}{41}) 
\end{align}

(Note: this is not a simple shift but a rotation.)

The processing of round constants, substitution, and rotation constitutes a permutation round. These permutation rounds are applied:

• 12 times for initialization,
• 8 times for each associated data block,
• 8 times for each plaintext block, and
• 12 times for tag generation.

Ascon in Excel

For demonstration and learning purposes, an implementation of the encryption in Excel was created, based on the original design.

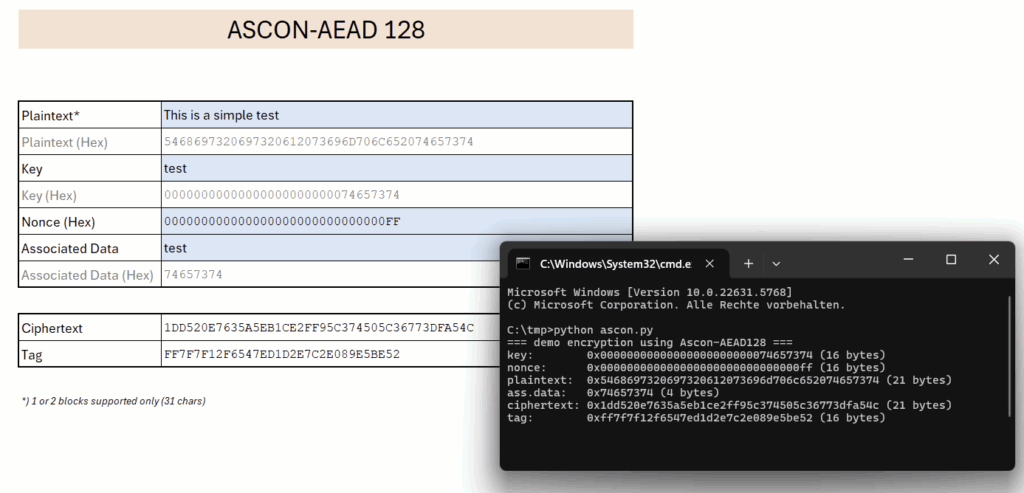
Download the Microsoft Excel file. No macros are used; however, due to the reliance on Lambda functions, the file will only run under Office 365 or Excel 2024.

_{SHA256: 69C4FB0318642D3438F5AF4565FBD90CB93DF26CFB27EECF867A62B4F28C2E14}