Auf dieser Seite wird eine Implementierung von Diffie-Hellman auf elliptischen Kurven in Excel präsentiert. Die Datei wird am Ende des Dokuments zum Download bereitgestellt. Selbtsverständlich dient diese allein zu Lernzwecken.

Zunächst werden die Parameter der elliptischen Kurve festgelegt. Anschließend lässt sich der vollständige Graph, der auf dem Generatorpunkt G basiert, visualisieren. Indem der Wert von n (hier 4) schrittweise manuell erhöht wird, können die entsprechenden Punkte auf der Kurve nach und nach durchlaufen werden. Aus technischen Gründen sollte der Wert von p maximal 101 betragen.

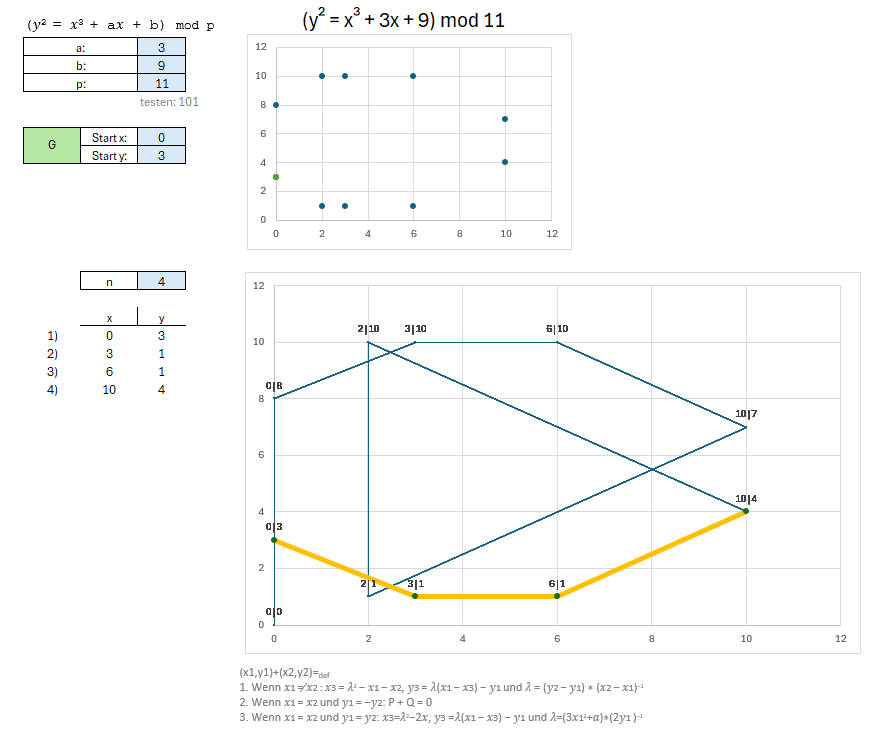
Neben der Visualisierung kann auf dem zweiten Registerblatt („ECDH“) der Schlüsselaustausch beideitig simuliert werden. Zu diesem Zweck wird auf beiden Seiten (A und B) jeweils ein Geheimnis a und b gewählt. In diesem Setting sollte das Geheimnis kleiner als 11 gewählt werden. Um einere größere Auswahl an Schlüsseln zu ermöglichen, kann hier das p auf 101 geändert werden. Auf Basis des gewählten Geheimnisses werden die resultierende Punkte der Kurve ermittelt und grafisch dargestellt.

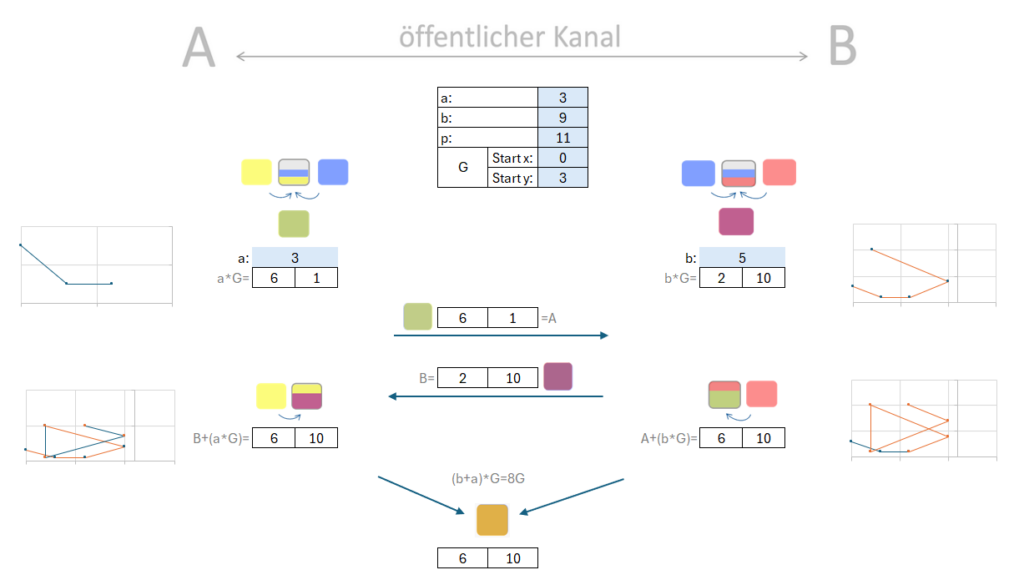
So zeigt sich am Ende das gleiche Ergebnis auf beiden Seiten. Das gemeinsame Geheimnis kann hierbei wahlweise x oder y sein.

Download der Microsoft Excel-Datei. Auf Makros wurde verzichtet; aufgrund der Lambda-Funktionen wird das Ergebnis jedoch nur unter Office 365 oder Excel 2024 lauffähig sein.

_{SHA256: D0524A7792DEC9F2D55659FB8C627A0FDC0407B8C029718E2FAF986800E85873}