SPHINCS+, or SLH-DSA, is one of the PQC schemes standardized by NIST in 2024. SLH-DSA is considered a particularly conservative, hash-based alternative to ML-DSA, offering long-term security and serving as a fallback in case weaknesses are discovered in lattice-based schemes.

However, to understand the scheme, some foundational concepts are helpful. The following sections therefore explain Lamport OTS, Merkle trees, Winternitz OTS, HORS, HORST, and FORS. Based on these, the hypertree underlying the scheme can be clearly understood.

This document uses screenshots from an Excel file, which is provided at the end of the document. Please note that the Murmur3 hash function is used in that file; while it does not provide cryptographic security, it is entirely sufficient for demonstration purposes.

Lamport OTS

The Lamport one-time signature (OTS) is not used directly in SPHINCS+, but it forms an essential foundation. It demonstrates how a signature can be constructed using nothing but a hash function, and how it can be verified without any knowledge of secret parameters. The underlying principle is remarkably simple.

For illustration, we use a hash function with a 32-bit output length; in practice, 256 bits are typical.

For each bit of the hash value, we generate a pair of two independent random values. With 32 bits, this results in 32 pairs, i.e., a total of 64 random values. Figure 1 (left) illustrates this by showing that the first group of 32 random values represents bit value 0, while the second group represents bit value 1.

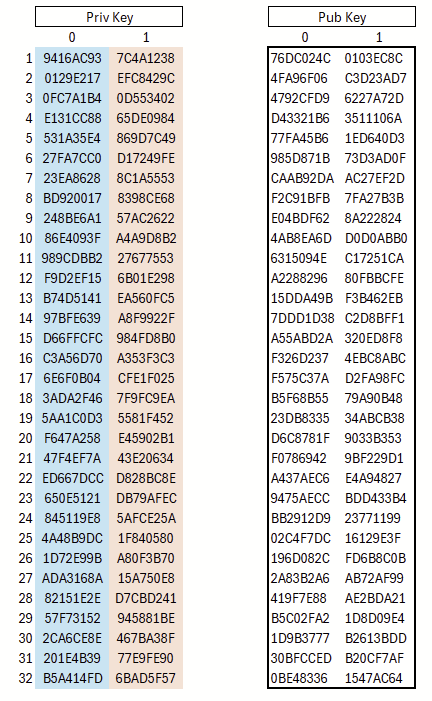
By applying a hash function once to each element in the left column, we obtain the corresponding element in the right column. The resulting 2×32 hash values form the public key, which can be published. Due to the preimage resistance of the hash function, it is not possible to compute the corresponding preimage from a given hash value; consequently, the private key cannot be derived from the public key.

With this, the key material is generated. Since this is a one-time signature scheme, exactly one signature can be created with a given public key. To generate a signature, the hash of the message to be signed is first computed. The bit string of this hash determines which private key components are revealed: if a bit is 0, the left component of the corresponding pair is published; if it is 1, the right component is published. For verification, the verifier hashes the disclosed values and compares them to the corresponding entries of the public key (left for 0, right for 1). If they all match, the signature is valid. The signature generation process is shown in Figure 2.

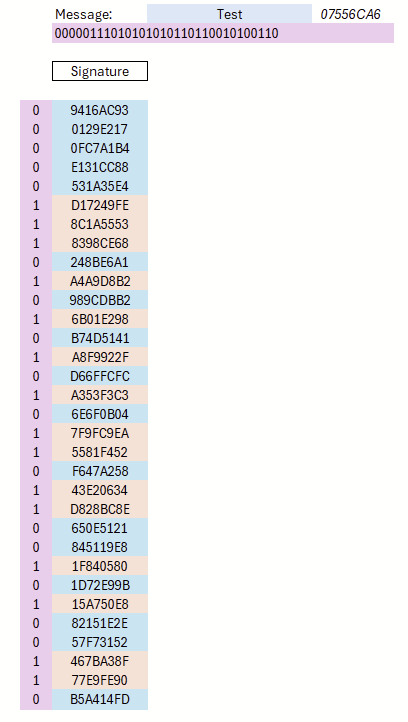
An obvious weakness of this scheme is that the public key serves exclusively for verifying a single signature. Another drawback is the comparatively large size of both the public key and the signature: when using SHA-256, this already requires 2×256 hash values.

Merkle Tree

To reduce the problem of large public keys, SPHINCS+ uses Merkle trees. The public keys are arranged as the leaves of a binary tree; each internal node is created by applying the hash function to the concatenation of its two child nodes. For example, if two child nodes A and B are given, the parent node is computed as H(A || B).

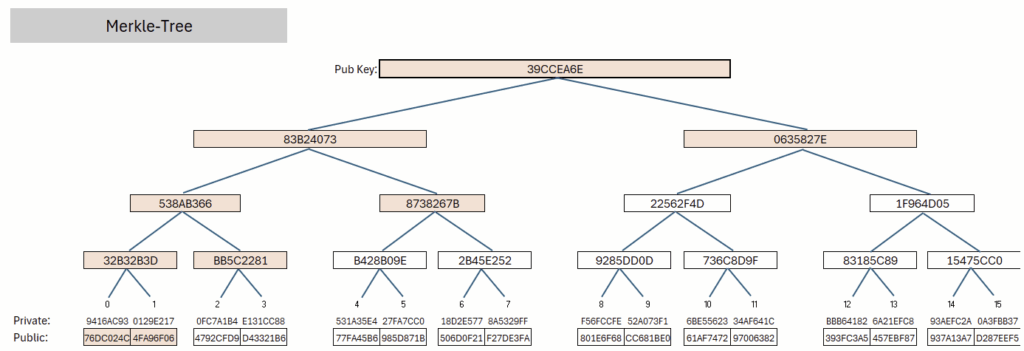
Figure 3 shows such a tree: starting from 16 randomly chosen private values, public values are generated using a hash function, forming the leaves of the tree. By pairwise combining adjacent nodes, a single public key is produced at the root, representing the entire tree.

To compute the public key at the root, the full tree must be constructed and processed; afterward, it is sufficient to keep only part of the values in memory. It is important to note that, when generating the signature, not all public values need to be revealed for the Merkle tree to be validated during signature verification. In Figure 3, a path from one leaf pair to the root is highlighted. Only these values are required to verify the correctness of the public key. Thus, a full publication of the Merkle tree is not necessary for verification; instead, only the path from the leaf to the root – including the corresponding sibling nodes – must be provided.

Winternitz OTS

Winternitz One-Time Signatures (W-OTS) are an advancement of the Lamport scheme and reduce the number of required hash values. However, the procedure is somewhat less intuitive than the Lamport approach.

The core idea: instead of signing each individual bit of the message separately, pairs of values are grouped together and processed jointly.

Let’s begin with a simple example. We generate a random starting value, for example 9416AC93, and repeatedly apply a hash function to it:

H(9416AC93) = 76DC024C
H(H(9416AC93)) = H(76DC024C) = 97028DBD
H(H(H(9416AC93))) = H(97028DBD) = F7E44484

The final value serves as the corresponding public key for the private starting value 9416AC93. This forms the hash chain:

9416AC93 → 76DC024C → 97028DBD → F7E44484

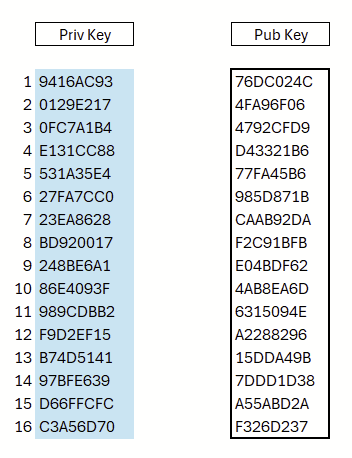
We repeat this process for 16 independent random values. These 16 starting values collectively form the private key; the respective endpoints of the chains serve as the corresponding components of the public key (see Figure 4).

The four columns represent the bit combinations 00, 01, 10, and 11. To create the signature, the (hash of the) message is read two bits at a time: each pair of bits determines the corresponding column, and the associated hash value stored in that column is revealed.

In the example, the binary representation begins with 10 11 00 01 110011 …; accordingly, the hash values from column 3, column 4, column 1, and column 2 are used for the signature in that order (see Figure 5).

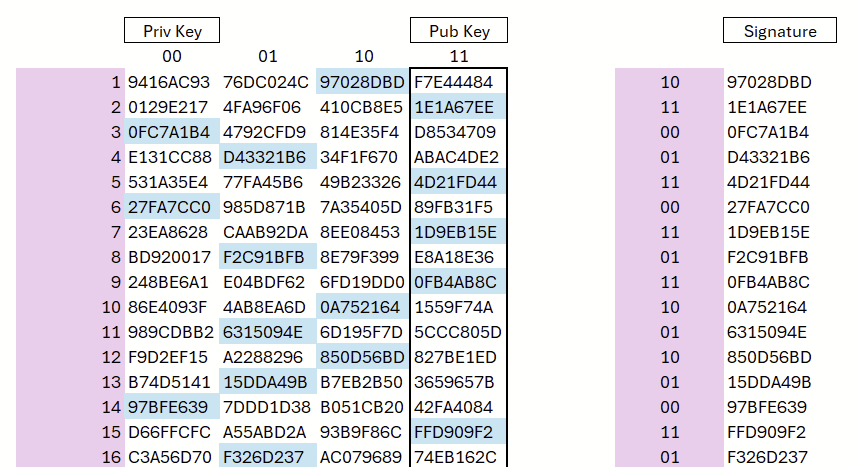
For signature verification, each revealed value is hashed 0 to 3 times depending on its position. If the result matches the reference value stored in the public key, the entry is considered valid. Example: the revealed value 97028DBD (row 1) is hashed once; if this produces F7E44484, as specified in the public key, it is correct.

Without additional protection, however, very small manipulations (such as one- or two-bit changes) could go unnoticed. For instance, an attacker could change the bits in row 1 from 10 to 11 and replace the value 97028DBD with the public-key value F7E44484 — the verification would not detect this. For this reason, the signature is augmented with a checksum. Put simply: if a value in one chain is shifted to the right, a corresponding shift to the left must occur elsewhere. An attacker cannot determine this counter-shift, since only the values further to the right are known to them, and the required earlier chain values cannot be computed backwards. This ensures that even single-bit modifications cannot go undetected. Figure 6 shows a WOTS signature including the checksum.

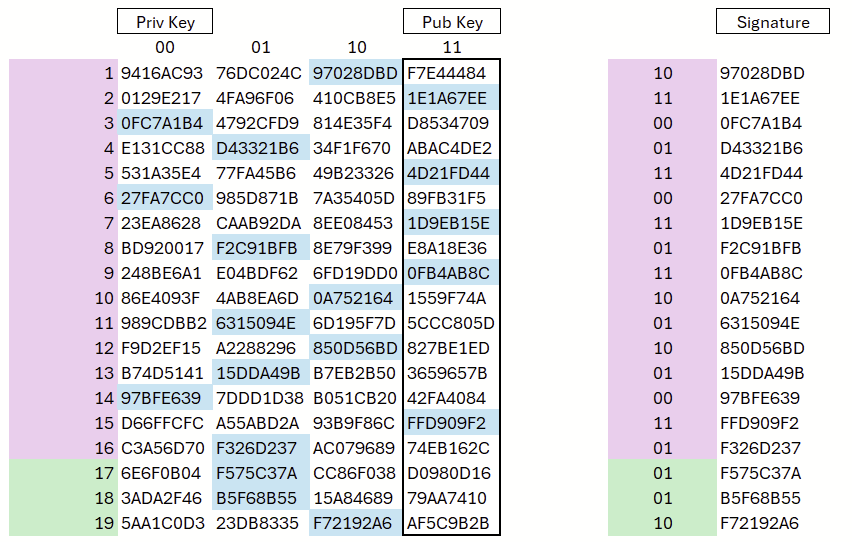
WOTS and WOTS+ are used in SPHINCS+ in the form described here. The “+” indicates that, before hashing, the input values are additionally combined with a mask via XOR. This technique facilitates security proofs, but it is not considered in detail here. In SPHINCS+/SLH-DSA, a Winternitz parameter of w = 16 is used: this corresponds to 4-bit blocks (hex digits); each WOTS+ chain therefore has 16 positions (0 to 15).

HORS / HORST

HORS (Hash to Obtain Random Subset) and its tree-based variant HORST are considered predecessors of FORS. FORS is used in SPHINCS+, whereas earlier SPHINCS versions (such as SPHINCS-256) still used HORST.

Lamport OTS and Winternitz OTS are true one-time signature schemes: with a single key pair, exactly one signature can be generated. HORS/HORST and FORS, on the other hand, are few-time signature schemes. This means that a key pair is not immediately consumed after producing the first signature, but can be reused for a small number of additional signatures.

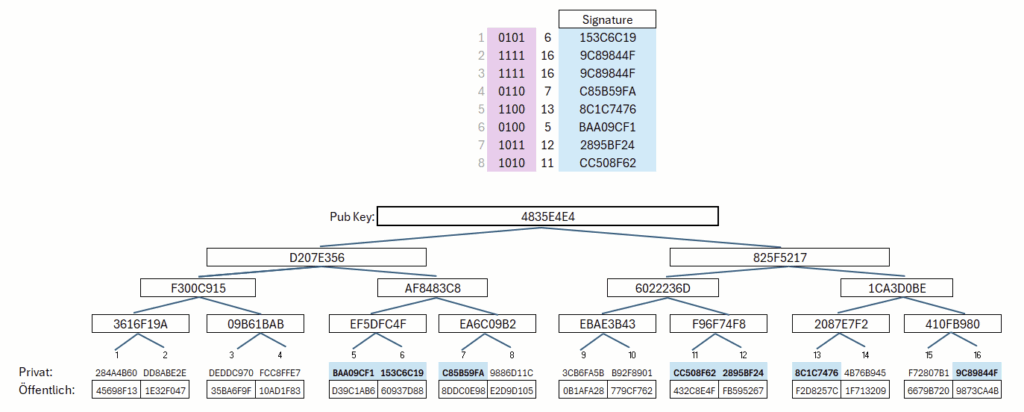
The procedure itself is comparatively simple. First, as in Lamport OTS, a set of random values is generated, and a public key is created for each value by applying a hash function (Figure 7).

---

From the hash of the message, a small subset of public hash values is deterministically selected and used as a sample. The corresponding private values at these positions are then revealed. In the example shown, 4 bits of the message are always used to deterministically select a private key; for a different message, a different set of private keys is selected accordingly. However, with repeated use, all private keys would gradually be revealed. The scheme is therefore not intended for such repeated use; its purpose is merely to ensure that limited reuse does not have immediately catastrophic consequences — unlike WOTS.

The process of signature generation, as well as the creation and selection of sample values, can be seen in Figure 8.

By combining this concept with a Merkle tree, we obtain HORST. In this construction, the public keys are organized in a tree structure so that, at the end, a single public key represents the entire tree. It is easy to see that, in this case, the leaves are selected based on the message. This is illustrated in Figure 9.

FORS

FORS (Forest of Random Subsets) is also a few-time signature scheme. While we previously always considered a single tree – shown with small height in the figures for illustration, but much taller in practice – FORS uses multiple small trees, i.e., a forest. The message is split into multiple parts; each tree is assigned exactly one part. Depending on this message part, a leaf in the corresponding tree is deterministically selected.

Step by step: consider Figure 10. If we divide the message into eight segments, each segment yields a 4-bit value. We assign each of these eight values to one tree and deterministically derive the leaf to be selected from each 4-bit value. In this example, we simply compute (value modulo 4) + 1.

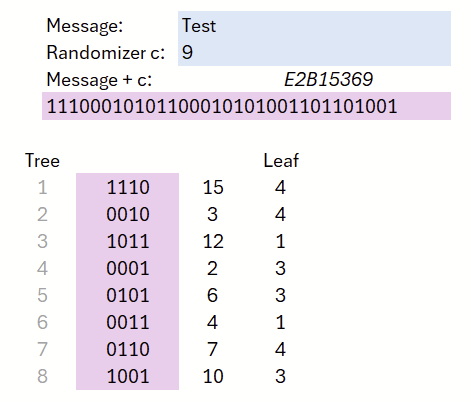
This results in the following assignments: Tree 1 → Leaf 4, Tree 2 → Leaf 4, Tree 3 → Leaf 1. Each tree corresponds to a Merkle tree: from a set of secret (private) values, public values are derived using a hash function and organized in a tree structure. Let us first examine these three trees in detail (Figure 11): in the first two trees, the fourth leaf was selected, and in the third tree, the first leaf. For these selected leaves, the corresponding private keys are revealed.

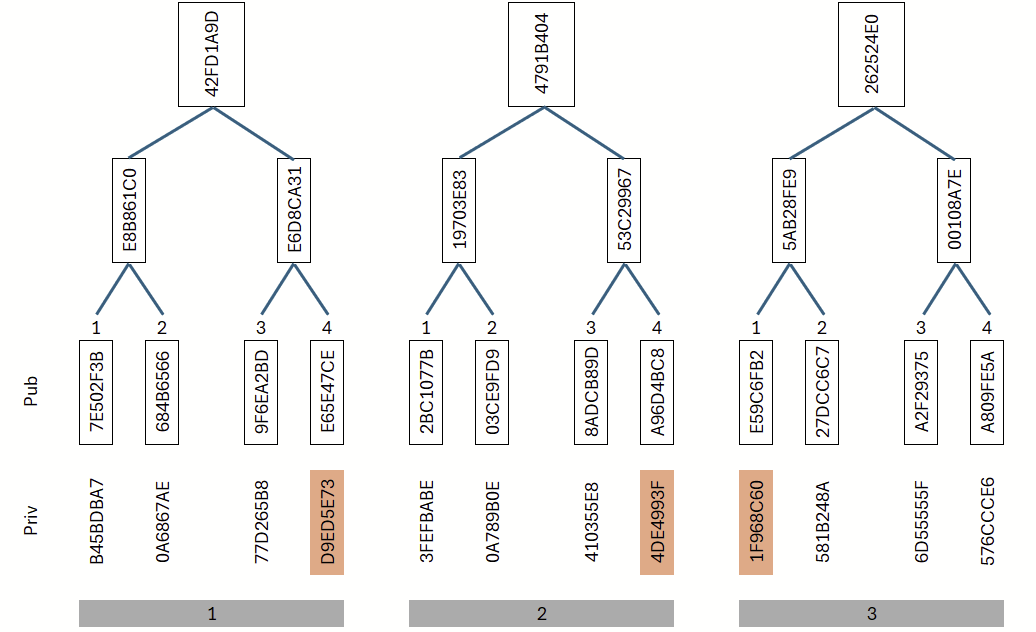
Each segment of the message is assigned to one tree; depending on its content, an appropriate leaf is selected in that tree. If the message changes, a different selection of leaves will likely result. The eight trees used are shown in Figure 12.

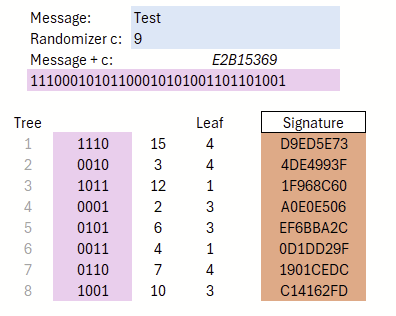
The selection of these leaves thus forms the signature of the message, which can be seen in Figure 13.

SPHINCS+

A hypertree is a Merkle tree made up of Merkle trees. It makes it possible to authenticate a very large number of signatures under a single public key — and to do so in a stateless manner, meaning without having to keep track of which leaves have already been used. The roots of the lower trees each serve as leaves of the next higher trees, up to the topmost root, which forms the public key. The trees that are linked together in this way are also called layers.

When a message is signed in SPHINCS+, a path in the hypertree is selected based on the value to be signed, leading down to a leaf. This leaf forms the transition to FORS. The actual signature is therefore produced using FORS, while the individual trees are linked and secured using Winternitz OTS.

The entire structure is constructed deterministically from a secret value. This ensures that the same tree is always generated and used for signature creation.

SHORT vs. FAST

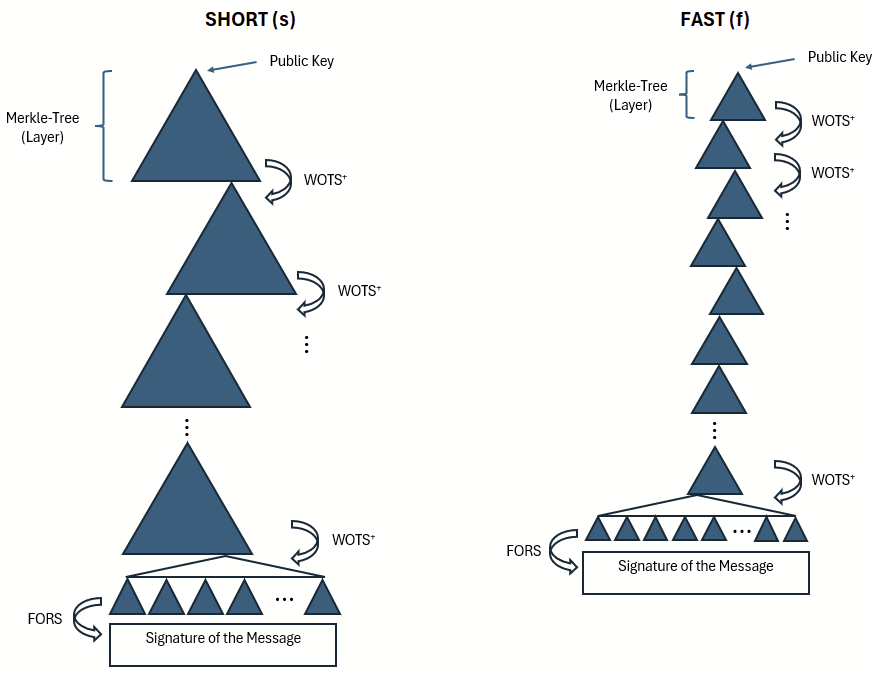
Looking again at Figure 14, we can observe that there are different ways to construct such a tree. Possible parameters include the height of the overall structure, the height of the individual Merkle trees, and the height and number of trees within FORS.

To compute the root of a Merkle tree, the entire tree must be built; the number of leaves grows exponentially, which means this process takes some time.

If we reduce the height of the Merkle trees, we then need more of them to achieve a comparable number of leaves. More trees, in turn, mean more signatures or more links between the trees. This increases the total signature size, because these linking elements need to be included.

In Figure 15, the SHORT and FAST variants are compared. Larger layers lead to shorter signatures but require longer computation times. Smaller layers result in more signatures, increasing their total size, but they can be computed faster.

Summary

To conclude, the individual pieces of the puzzle shall be assembled into a coherent picture. To create a public key, a secret initial value (seed) is first required. From this secret, the Merkle tree of the top layer is deterministically generated; its root forms the public key.

To generate a signature, a hash value is computed from the message (optionally using a random value). One part of this hash value uniquely determines the path through the hypertree. Following this path requires constructing all necessary layers in full. The layers are linked using WOTS+. A signature must include both the path through each layer and the corresponding WOTS+ signatures.

It is assumed that each message selects a different path in the hypertree (there are roughly 2^64 leaves in total), making the probability of ending up in the same FORS tree twice negligible — at least up to a certain number of signatures.

At the lowest layer (final layer), a forest of “small” trees is generated for FORS. The other part of the hash value is then used to select trees and leaves within FORS. The corresponding secret values of the selected leaves are revealed; together with their authentication paths, they form the signature of the message.

For verification, the derived hash values and the public key are first checked within FORS; then the WOTS+ signatures of each layer are verified one after another until the top layer is reached. Finally, it is checked whether the public key can be correctly derived from the tree. If so, the signature is valid.

SPHINCS+ in Excel

The concepts presented here have been implemented in Excel as an illustrative example. In the demo, however, the linking of layers using WOTS+ was omitted for obvious reasons. The path through a four-layer hypertree is computed and displayed, as well as the creation of the signature using FORS with five trees.

No macros were used; however, due to the use of lambda functions, the result will only run under Office 365 or Excel 2024.

No macros were used; however, due to the use of lambda functions, the result will only run under Office 365 or Excel 2024.