Dilithium, bzw. nach der Standardisierung ML-DSA genannt, basiert auf derselben Falltür (Module Learning with Errors) wie Kyber (bzw. ML-KEM). Wer somit das Verfahren besser verstehen möchte, sollte sich zunächst mit der Algebra auf Polynomringen befassen. Diese ist im Artikel zu Kyber bereits sehr ausführlich dargestellt worden.

Somit arbeitet Dilithium mit Matrizen und Vektoren, deren Komponenten überwiegend Polynome vom Grad n sind. Dabei werden die Komponenten stets modulo q reduziert. In der hier dargestellten vereinfachten Variante sind die Polynome vom Grad 3 und werden somit durch ein Polynom vierten Grades dividiert; die Komponenten werden hingegen modulo 61 reduziert.

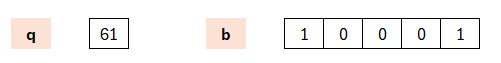
Im echten Dilithium ist der Grad (n) 255; somit ist b = 2^256+1 und q ist auf 8380417 gesetzt.

Weitere Voraussetzungen

Es gibt drei wesentliche Dinge, die über Dilithium vorab verstanden sein müssen: die zentrierte/symmetrische Moduloberechnung, die Verwendung von HighBits/LowBits und die SampleInBall-Funktion. Diese werden im Folgenden näher erläutert.

Zentrierte/symmetrische Moduloberechnung

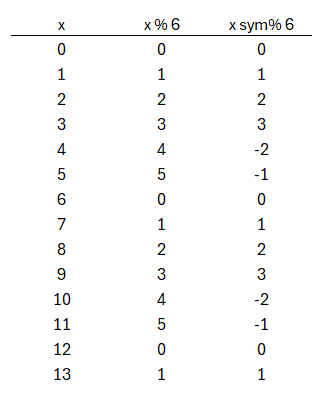
Beim üblichen Modulo-Rechnen, zieht man den Modulus (hier q) so häufig ab, bis man bei einem Wert darunter landet. Beispielsweise ist 8 modulo 6 = 2, da 8 – (1*6) = 2 ist. Somit ergeben sich die Werte von 0 bis 5, denn ab der 6 wären wir wieder bei der 0.

Beim zentrierten/symmetrischen Modulo, ziehen wir schon ab der Hälfte das q ab. Bleiben wir bei dem Beispiel mit der 6, dann passiert bei 0, 1, 2 und 3 noch nichts. Aber bei 4 sind wir über der Hälfte und ziehen daher einmal die 6 ab: 4 – (1*6)= -2. Und so landen wir mit der 5 bei der -1 usw.

\text{Sei } a \in \mathbb{Z}, \; q \in \mathbb{N} 
\\r = a \bmod q \\[6pt]
a \bmod^{\ast} q =
\begin{cases}
r, & 0 \leq r < \tfrac{q}{2}, \\[6pt]
r - q, & \tfrac{q}{2} \leq r < q.
\end{cases}

HighBits/LowBits

Auch wenn es in Kyber schon erforderlich war (…dort konnte man es jedoch etwas leichter verschweigen) kommt in Dilithium die Aufspaltung in High- und LowBits zur Anwendung. Zunächst hierfür ein Beispiel. Nehmen wir eine beliebige Zahl wie r=20 und einen Wert α=3. Dieses r=20 können wir auch durch Vielfache der 3 zuzüglich einem Rest ausdrücken:

20 = 6 * 3 + 2

Bei diesem Beispiel entspricht der Faktor vor der 3 (α) den HighBits und der Rest den LowBits. Also HighBits(20,3)=6 und LowBits(20,3)=2. Auch wenn in diesem Beispiel nicht direkt ersichtlich: Auf diese Weise lassen sich auch große Zahlen durch kleine Werte ausdrücken. Im echten Dilithium (ML-DSA-44) wird beispielsweise ein α von 95232 verwendet. Somit würde sich der Nachfolger 95233 durch die High-/LowBits (1,1) eindeutig ausdrücken lassen. Das ist sehr kompakt.

Die Aufspaltung in High- und LowBits dient allerdings nicht der Kompression, sondern stellt sicher, dass die durch die geheimen Schlüssel eingebrachten Störungen (Noise) die LowBits betreffen, während die HighBits im Idealfall unverändert bleiben.

Im echten Dilithium wird an dieser Stelle zusätzlich ein Hint-Vektor genutzt. Dieser enthält wenige Zusatzinformationen, die genau an den Positionen eine Korrektur erlauben, an denen die Rauschanteile sonst zu unterschiedlichen HighBits führen würden. So wird sichergestellt, dass Sender und Empfänger bei der Verifikation dasselbe Ergebnis erhalten.

Allerdings kann das im Verfahren dann unübersichtlich werden, wenn zusätzlich noch die symmetrische Moduloberechnung ins Spiel kommt. An dieser Stelle wurde die ursprüngliche Abbildung durch die decompose-Funktion ergänzt. Hierbei wurde q=6 gesetzt und α=3 (alpha).

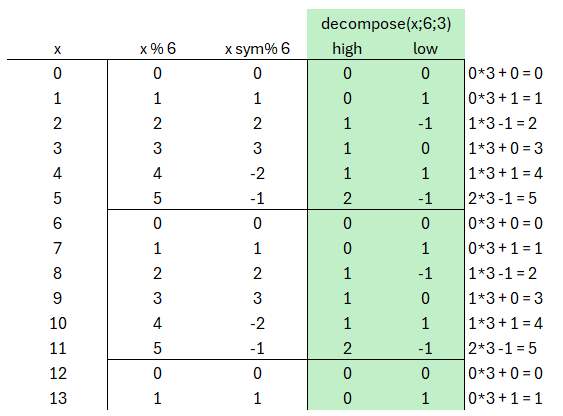
So wird der Wert 5 eben nicht durch 1*3+2 ausgedrückt, sondern eben durch 2*3-1.

Das ist ohne Frage nicht sehr intuitiv, weshalb es an manchen Stellen im Verfahren schwierig ist, die Operationen selbst nachzurechnen. Wer das gerne selbst ausprobieren möchte, kann sich die Definition der decompose-Funktion zur Zerlegung in High- und LowBits aus dem Standard näher anschauen und/oder die decompose-Funktion im Excel-Sheet verwenden.

function DECOMPOSE(r, q, gamma2):
    alpha := 2 * gamma2
    r_plus := r mod q                     
    r0 := CENTERED_MOD(r_plus, alpha)       

    if (r_plus - r0) == (q - 1):
        r1 := 0
        r0 := r0 - 1
    else:
        r1 := (r_plus - r0) / alpha         
    return (r1, r0)

SampleInBall-Funktion

Im Laufe des Verfahrens muss ein Vektor mit Komponenten aus der Menge {-1, 0, 1} generiert werden. Also z. B. so etwas wie

[0, -1, 1, 1, 0, 0, 0 …, 0, 1]

Das Verfahren fordert dabei, dass eine feste Menge von -1 und 1 eingebaut werden, die restlichen Komponenten bleiben 0. So steht man also vor dem Problem, dass genau tau-viele¹ Werte von 0 auf 1 oder -1 geändert werden sollen. Zusätzlich bestehen die Anforderungen, dass es zufällig aussehen, aber dennoch deterministisch generiert sein muss. Das bedeutet, aus demselben Eingabewert soll stets der gleiche Vektor mit 0, 1 und -1 entstehen.

# SampleInBall: erzeugt Vektor c ∈ {−1,0,1}^n mit Hamming-Gewicht tau
# b: Seed (Byte-Array) für Zufallsquelle
# n: Länge des Vektors (z. B. 256)
# tau: Anzahl Nicht-Null-Koeffizienten (≤ n)
function SAMPLE_IN_BALL(b, n, tau):
    c[0..n-1] := 0
    RNG.Seed(b)

    for i from (n - tau) to (n - 1):
        j := RNG.UniformInteger(0, i)         
        s := RNG.UniformInteger(0, 1)         

        c[i] := c[j]                          
        if s == 0:
            c[j] := +1
        else:
            c[j] := -1
    end for

    return c

Schlüsselerzeugung

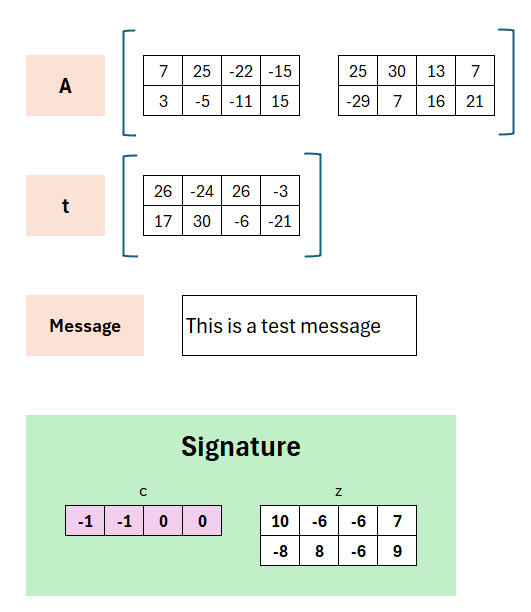
Das Schlüsselmaterial besteht aus einer Matrix A, den privaten Komponenten s₁ und s₂ und dem Ergebnis t = A * s₁ + s₂.

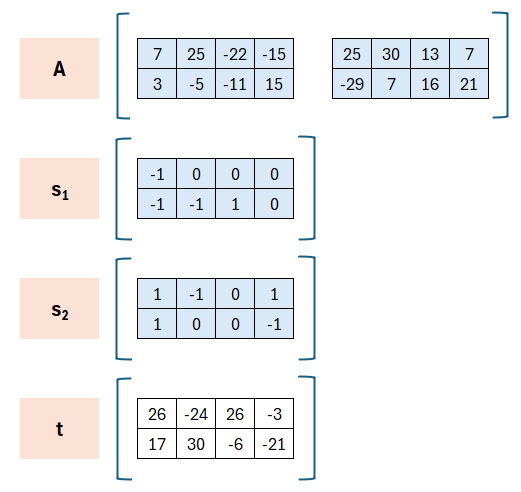
Hierbei ist (A,t) der öffentliche Schlüssel und (s₁, s₂) der private Schlüssel. Mittels dieser Werte wird somit die Signatur erzeugt, während der Empfänger mit (A,t) in der Lage sein muss die Signatur zu prüfen.

Die Komponenten von A können beliebig (modulo q) gewählt werden, die Komponenten von s₁ und s₂ sollen eher klein ausgewählt werden. Das Ergebnis t ergibt sich aus der Wahl. Im „echten“ Dilithium wird A durch ein seed und eine Hashfunktion erzeugt.

Signaturerzeugung

Die Signaturerzeugung ist die Komponente, die am schwierigsten zu verstehen ist. Das liegt vermutlich darin begründet, dass, anders als bei anderen Verfahren, passende Zufallsparameter erst gesucht und gefunden werden müssen. Es ist daher nicht so, dass das Verfahren in jedem Fall direkt gelingt. Es gibt eine gewisse Wahrscheinlichkeit, dass die Parameter so unglücklich (zufällig) gewählt worden sind, dass ein weiterer Versuch mit anderen Parametern erforderlich ist.

Im „echten“ Dilithium passiert dies seltener, da die Größe der Polynome mehr Spielraum lassen. In der hier dargestellten verkleinerten Variante können mehr Iterationsschritte erforderlich sein, um die Signatur zu erzeugen. An dieser Stelle wird nur der positive Fall dargestellt, im Excel-Dokument unten können jedoch auch die Fehlversuche gesichtet werden.

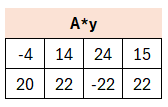
Das Verfahren startet damit, dass ein Vektor y zufällig gewählt wird. Hierbei gibt es bzgl. der Wahl der Komponenten die Einschränkung, dass diese in einem bestimmten Intervall liegen (genauer aus: (-gamma1,gamma1]).

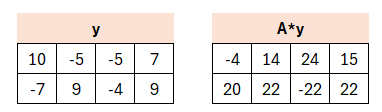
Die Matrix A, als Teil des öffentlichen Schlüssels, wird mit y multipliziert. Im Anschluss werden die HighBits aus dem Produkt extrahiert. Der α-Wert (das oben beschriebene Vielfache) ist im Verfahren festgeschrieben und in unserem Fall wird 2*gamma2 also auf 2*10 gesetzt.

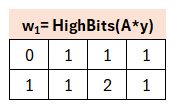
Wer sich nun wundert, wie bei einem α von 20 aus der 14 eine 1 wird: dies liegt, wie oben erwähnt, an zentrierten Modulo. Dabei ist alles zwischen 11 und 30 eine 1. Die -22 ist kongruent zu 39, weshalb hier eine 2 gesetzt wird.

Nun wird aus diesem w₁ eine Zeichenkette gebildet, die der Nachricht (hier: „This is a test message“), also dem zu signierenden Dokument, angehängt wird. Wir konkatinieren also diese Werte an das zu signierende Dokument und erstellen einen Hashwert.

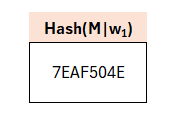
Wie an dieser Stelle der Hash generiert wird, wird etwas weiter unten erläutert. Wir stellen uns an dieser Stelle vor, es wäre das Ergebnis einer kryptografisch sicheren Hashfunktion mit einer entsprechend sicheren Ausgabelänge.

Bisher haben wir nur Dinge getan, die jeder könnte, denn A ist der öffentliche Schlüssel und y wurde zufällig gewählt. Der Rest war eine deterministische Berechnung. Das bedeutet, der eigentliche Signaturschritt muss jetzt kommen.

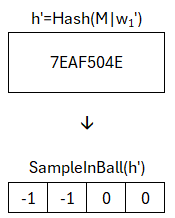
Die Signatur besteht aus zwei Teilen: einer Challenge und einer Response. Die Challenge ist das Ergebnis der SampleInBall-Funktion. Zur Erinnerung: Diese Funktion soll deterministisch ein Vektor mit Komponenten aus {-1, 0, 1} erzeugen. Bei gleichem Seed soll der gleiche Vektor erzeugt werden. Als Seed wird die Ausgabe der Hashfunktion von oben verwendet. Das bedeutet, die Nachricht verkettet mit w₁ wird gehasht und geht als Seed in die SampleInBall-Funktion, welches einen solchen Vektor generiert.

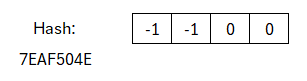
In diesem Fall ist der Vektor [-1 -1 0 0] entstanden. Aber auch bis hier hin, hätte dies grundsätzlich noch jeder ausführen können, da Hashfunktion und SampleInBall-Funktion im Standard festgeschrieben sind.

Somit besteht die Signatur aus dem letzten Schritt: die Generierung von z. Dabei ist z definiert als das Produkt von c mit s₁ (privater Schlüssel) und Addition mit y.

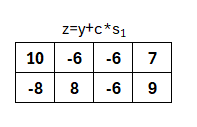
Somit ist z der Teil der Signatur, der nur mit Kenntnis von s₁ gültig erzeugt werden kann. Wie die Gültigkeit geprüft und die Signatur verifiziert wird, kommt entsprechend im nächsten Abschnitt.

Zusammenfassend besteht die Signatur aus der Challenge c und der Response z, welche auf Basis des geheimen Schlüssels erzeugt wurde.

Wer sehr weit vorausblicken kann, wird feststellen, dass zur Signaturprüfung y dauerhaft verbleibt und eine Unbekannte ist. Deshalb ist die Auswahl von y so schwierig und erfordert möglicherweise mehrere Iterationen: Sind die Komponenten von y ungeschickt gewählt, könnte dies entweder Rückschlüsse auf den privaten Schlüssel s₁ erlauben oder dazu führen, dass die Verifikationsprüfung fehlschlägt. Im „echten“ Dilithium wird daher zusätzlich ein Hint-Vektor verwendet. Dieser sorgt dafür, dass trotz der unvermeidlichen Rauschanteile bei der Berechnung dieselben HighBits rekonstruiert werden können, sodass die Signaturprüfung zuverlässig gelingt. Aber kommen wir zunächst genau dorthin: zur Überprüfung der Signatur.

Signaturprüfung

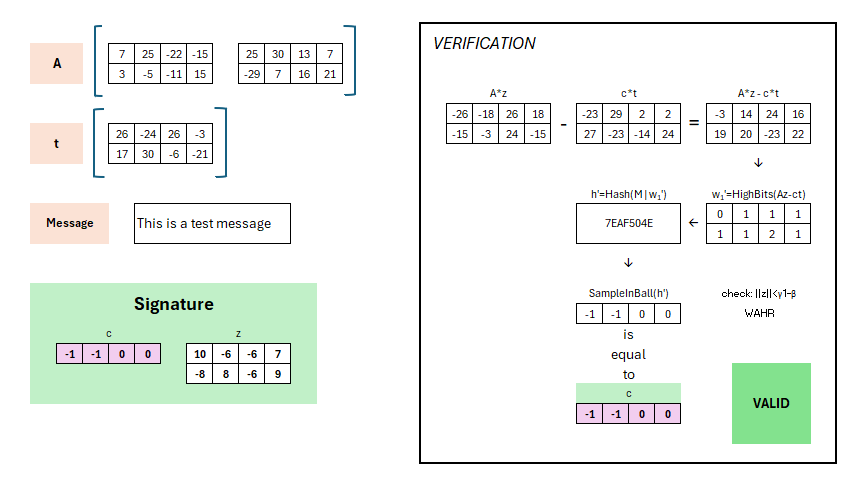
Schauen wir uns zunächst an, was wir auf Seite des Empfängers haben. Hier steht der öffentliche Schlüssel bestehend aus (A,t) zur Verfügung, die Nachricht „This is a test message“, die signiert wurde, und natürlich die Signatur selbst, bestehend aus (c,z).

Zur Signaturerzeugung wird A*z – c*t berechnet. Warum genau, lässt sich später etwas leichter zeigen. An dieser Stelle schauen wir uns erstmal das Ergebnis an.

Wenn wir das Ergebnis nun mit unserem vorherigen A*y aus dem Signaturprozess vergleichen…

… dann stellen wir fest, dass diese verschieden sind. Aber wenn wir genau hinschauen sehen wir möglicherweise, dass der Unterschied nicht so groß ist. Die Abweichungen sind vergleichsweise gering. Diese fänden also eher im LowBit-Bereich statt. So hätten wir die Hoffnung, dass der HighBit-Bereich identisch ist.

Schauen wir uns diesen an, dann bestätigen sich unsere Hoffnungen. Wir erhalten ein w₁' welches identisch zum w₁ aus der Signaturerstellung ist. Auch wenn wir y nicht herausrechnen konnten, war dieses so gewählt, dass es keine Auswirkungen auf den HighBit-Bereich hat. Dieses w₁' wird in gleicher Weise mit der Nachricht verbunden, gehasht und als Seed in die SampleInBall-Funktion gegeben.

Wir können nun prüfen, ob das Ergebnis aus der SampleInBall-Funktion identisch mit der Challenge aus der Signatur ist. Dies ist der Fall. Damit ist die Signatur erfolgreich überprüft und gültig. Die zusätzliche Überprüfung ist nur der Vollständigkeit aufgeführt und soll vor einem Angriff mit zu großem z schützen.

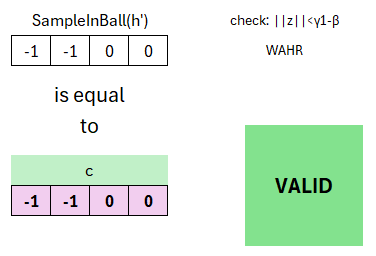
Ändern wir die Nachricht, führe dies zu einer anderen SampleInBall-Ausgabe und somit würde der Signaturüberprüfungsprozess fehlschlagen.

Korrektheit

Die Korrektheit des Verfahrens ist nicht ganz einfach darzustellen. Wenn wir jedoch beim Verifikationsprozess starten und die Variablen immer weiter auflösen, bleibt am Ende A*y-c*s₂ übrig.

\begin{aligned}
w_1'= Az - ct 
&= A(y + cs_1) - ct \\[6pt]
&= Ay + Acs_1 - c(As_1 + s_2) \\[6pt]
&= Ay + cAs_1 - cAs_1 - cs_2 \\[6pt]
&= Ay - cs_2 \, .
\end{aligned}

Das ursprüngliche w₁ bestand hingegen nur aus dem Produkt von A mit y.

w_1 = Ay

Damit das Verfahren funktioniert, werden die Parameter so gewählt, dass in Bezug auf die HighBits dasselbe Ergebnis berechnet wird. Im Nachgang entsteht der gleiche Hashwert und dasselbe Ergebnis der SampleInBall-Funktion.

\begin{aligned}
\mathrm{HIGHBITS}(Ay - cs_2, 2\gamma_2) = \mathrm{HIGHBITS}(Ay, 2\gamma_2) \, 
\end{aligned}

Mehr Informationen zur Korrektheit finden sich in diesem Dokument.

Implementierung in Excel

Zur Demonstration des Verfahrens wurde die hier vorgestellte vereinfachte Version in Excel umgesetzt. Wie bereits erläutert, erfordert Dilithium jedoch den Einsatz einer Hashfunktion. Zu diesem Zweck wurde die Hashfunktion MurmurHash3 implementiert. Es sei an dieser Stelle darauf hingewiesen, dass es sich um keine kryptografische Hashfunktion handelt; im „echten“ Dilithium wird SHAKE-128/256 hierfür verwendet. Aufgrund der 4-Byte-Ausgabelänge war diese jedoch gut für diesen Zweck geeignet. Sie wurde zusätzlich zu einem PRNG ausgebaut, um seed-gesteuert Zufallsbytes zu erzeugen.

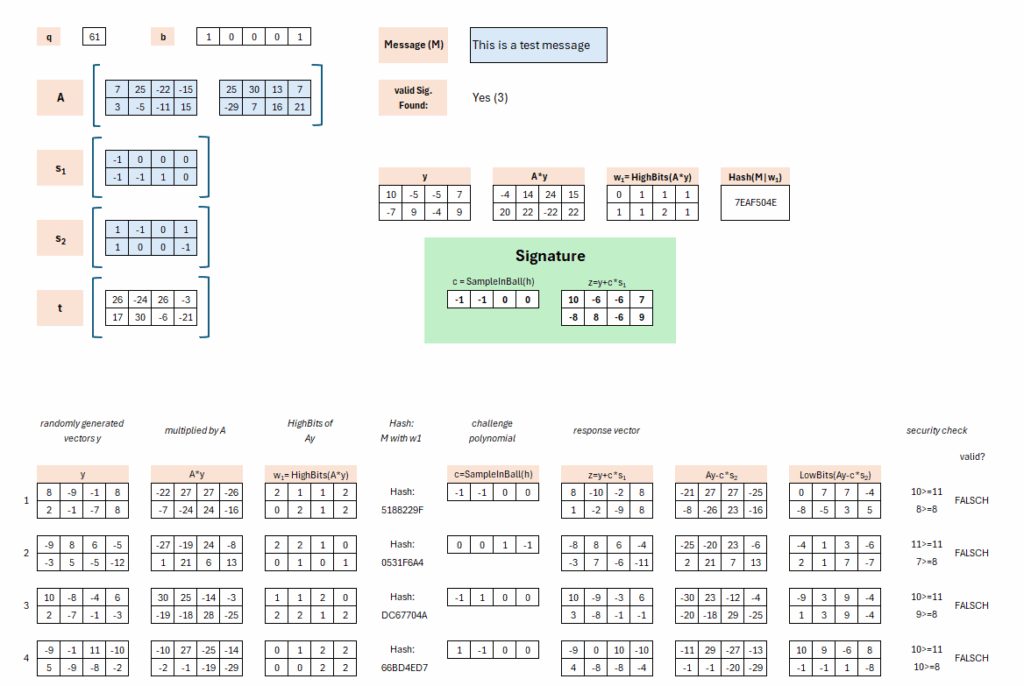
Download der Microsoft Excel-Datei. Auf Makros wurde verzichtet; aufgrund der Lambda-Funktionen wird das Ergebnis jedoch nur unter Office 365 oder Excel 2024 lauffähig sein.

_{SHA256: 2D5EFC91119377CC8F9AC4A037EB275FAB8F64061E56D6D038EAFE8D8B439BE7}

1. _{Tatsächlich wird im Verfahren diese Anzahl über den griechischen Buchstaben tau festelegt und deshalb auch hier verwendet.} ↩︎