Dilithium, or after standardization called ML‑DSA, is based on the same „Module Learning with Errors“ (MLWE) trapdoor as Kyber (or ML-KEM). If you want to understand the scheme better, you should first deal with the algebra on polynomial rings. That is already discussed in depth in the article on Kyber.

Thus Dilithium works with matrices and vectors whose components are mostly polynomials of degree n. The components are always reduced modulo q. In the simplified variant shown here, the polynomials are of degree 3 and hence divided by a fourth-degree polynomial; meanwhile the components are reduced modulo 61.

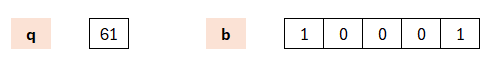
In the „real“ Dilithium the degree (n) is 256; thus b=2^256 + 1 and q is set to 8380417.

Further prerequisites

There are three essential things which must be understood in advance for Dilithium: the centered/symmetric modulo computation, the use of HighBits/LowBits, and the SampleInBall function. These are explained in the following.

Centered/Symmetric modulo computation

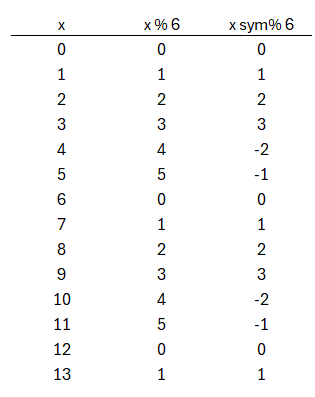
In ordinary modulo arithmetic, one subtracts the modulus (here q) as many times as needed until one lands in a value below the modulus. For example 8 modulo 6 = 2, since 8−(1×6)=2. Thus one obtains the values from 0 to 5 (because at 6 you would wrap back to 0).

In the centered/symmetric modulo, you subtract from the modulus already at half. Staying with the example modulus = 6, then for 0, 1, 2 and 3 nothing changes. But for 4 you are above half (6/2=3) and thus subtract 6: 4−6 = −2. And similarly 5 becomes −1 etc.

\text{Let}~ a \in \mathbb{Z}, \; q \in \mathbb{N} 
\\r = a \bmod q \\[6pt]
a \bmod^{\ast} ~~q =
\begin{cases}
r, & 0 \leq r < \tfrac{q}{2}, \\[6pt]
r - q, & \tfrac{q}{2} \leq r < q.
\end{cases}

HighBits/LowBits

Although this already was required in Kyber (… there you could somewhat more easily gloss over it), in Dilithium the splitting into HighBits and LowBits is applied. First an example: take an arbitrary number like r=20 and a value α=3. Then we can express r=20 through multiples of 3 plus a remainder:

20 = 6 × 3 + 2

In this example the factor before the 3 (i.e., 6) equals HighBits(20, 3) and the remainder equals LowBits(20, 3).

Even though in this example it’s not immediately visible: in this way even large numbers can be expressed by smaller values. In the real Dilithium (ML-DSA-44) for example an α=95232 is used. Then the successor 95233 would be expressed by HighBits/LowBits as (1, 1) uniquely. That is very compact.

However, the splitting into HighBits and LowBits is not used for compression, but ensures that the disturbances (noise) introduced via the secret keys only affect the LowBits, while the HighBits ideally remain unchanged.

In the real Dilithium a „hint-vector“ is used at this point. This contains a few extra pieces of information that allow correction exactly at those positions where the noise parts would otherwise cause different HighBits. This ensures that sender and receiver in verification obtain the same result.

But this can become confusing in the procedure once the symmetric modulo computation comes into play. At this point the original mapping is supplemented by the decompose-function. Here q=6 is set and α=3.

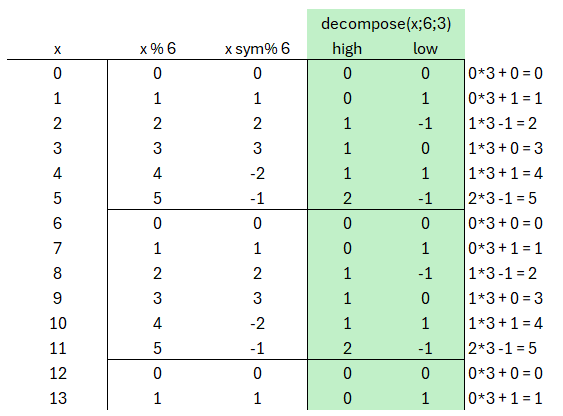
So the value 5 is not expressed as 1×3+2, but rather as 2×3−1. This is admittedly not very intuitive, which is why it can be difficult to manually compute the operations in some places of the scheme. If you want you can experiment with the definition of the decompose function for splitting into HighBits/LowBits from the standard and/or use the decompose function in the Excel sheet.

function DECOMPOSE(r, q, gamma2):
    alpha := 2 * gamma2
    r_plus := r mod q                     
    r0 := CENTERED_MOD(r_plus, alpha)       

    if (r_plus - r0) == (q - 1):
        r1 := 0
        r0 := r0 - 1
    else:
        r1 := (r_plus - r0) / alpha         
    return (r1, r0)

SampleInBall-Function

In the course of the scheme, a vector must be generated whose components are drawn from the set {−1,0,1}. For example something like: [0,−1,1,1,0,0,0 …,0,1]

The procedure requires that exactly τ many non-zero entries of −1 or +1 must be included, the remaining components stay 0. So one is faced with the problem of flipping exactly τ¹ many zeros into ±1. Additionally the requirements are that it should look random, but still be deterministically generated. That means: from the same input you always obtain the same vector with 0,1,−1.

# SampleInBall: produces vector c ∈ {−1,0,1}^n with Hamming-weight tau
# b: seed (byte-array) for RNG
# n: length of vector (e.g., 256)
# tau: number of non-zero coefficients (≤ n)
function SAMPLE_IN_BALL(b, n, tau):
    c[0..n-1] := 0
    RNG.Seed(b)

    for i from (n - tau) to (n - 1):
        j := RNG.UniformInteger(0, i)         
        s := RNG.UniformInteger(0, 1)         

        c[i] := c[j]                          
        if s == 0:
            c[j] := +1
        else:
            c[j] := -1
    end for

    return c

Key Generation

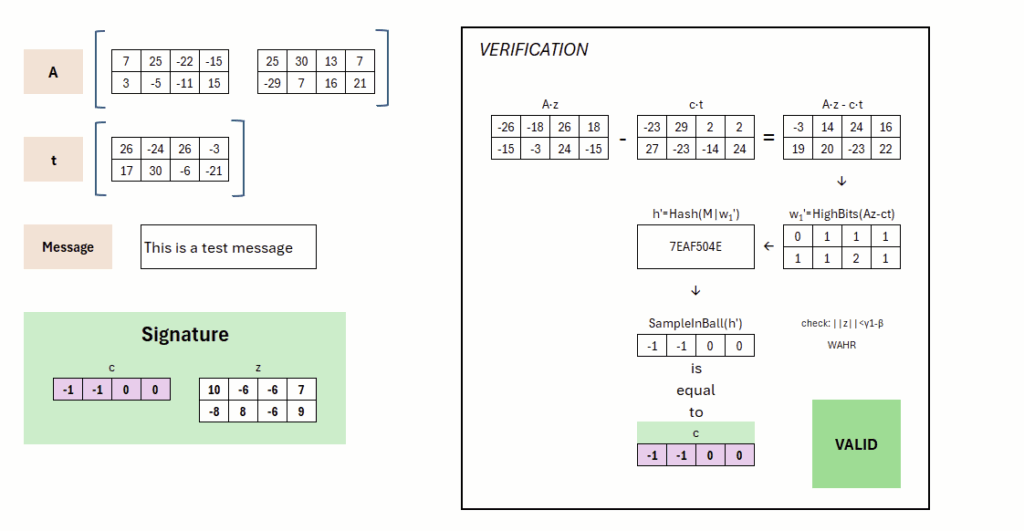
The key material consists of a matrix A, the private components s₁ and s₂​, and the result t=A⋅s₁+s₂.

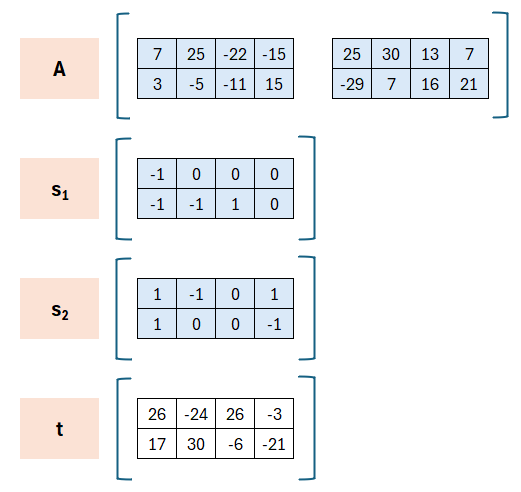
Here (A,t) is the public key and (s₁,s₂) is the private key. Using these values the signature is generated, while the receiver with (A,t) must be able to verify the signature.

The components of A may be chosen arbitrarily (mod q), the components of s₁​ and s₂​ should rather be small. The result t follows from the choices. In the „real“ Dilithium A is generated via a seed and a hash-function.

Signature Generation

Signature generation is the component that is hardest to understand. This is presumably because, unlike in other schemes, fitting random parameters must first be searched for and found. It’s therefore not so that the scheme always succeeds directly. There is a certain probability that the parameters were chosen so unfavourably (randomly) that another attempt with different parameters is required.

In the „real“ Dilithium this happens less often, because the size of the polynomials leaves more leeway. In the simplified variant shown here more iteration steps may be required to generate the signature. At this point only the positive (successful) case is shown; in the Excel document below however the failed attempts can also be viewed.

The procedure starts with choosing a vector y at random. Here the restriction concerning the choice of the components is that they lie in a certain interval (more precisely: (−γ1,γ1] ).

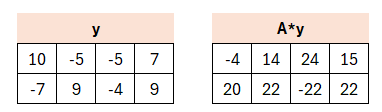
The matrix A, as part of the public key, is multiplied by y. Then the HighBits are extracted from that product. The α-value (the multiple described above) is fixed in the scheme and in our case is set to 2×γ₂​ which here is 2×10.

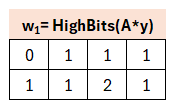
One might wonder, how from an α of 20 a 14 becomes a 1: this is due, as mentioned above, to the centered modulo operation. Everything between 11 and 30 becomes 1. The -22 is congruent to 39, therefore here a 2 is set.

Now from this w₁​ a character-string is formed which is appended to the message (here: „This is a test message“) i.e., the document to be signed. We therefore concatenate these values to the message to be signed and compute a hash.

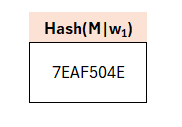
As to how exactly the hash is generated is explained a bit further below. At this point we imagine it to be the output of a cryptographically secure hash function with a corresponding output length.

Up to now we have only done things that anyone could do, since A is public and y was chosen randomly. The rest was a deterministic computation. That means now the actual signature step must come. The signature consists of two parts: a challenge c and a response z. The challenge is the output of the SampleInBall function. Reminder: this function should deterministically produce a vector with components from {−1,0,1}. As seed we use the output of the hash function from above. This means: the message concatenated with w₁ is hashed and used as seed in the SampleInBall function, which generates such a vector.

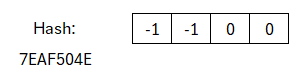
In this case the vector is [−1,−1,0,0]. But even at this point, up to here anyone could in principle have done it, since the hash-function and SampleInBall function are fixed in the standard.

Thus the signature consists of the final step: the generation of z. Here z is defined as the product of c with s₁​ (private key) plus y.

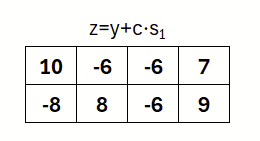
So z is the part of the signature that can only be validly created with knowledge of s₁. As to how validity is checked and the signature is verified, we come to that in the next section.

In summary the signature consists of the challenge c and the response z, which was generated based on the secret key.

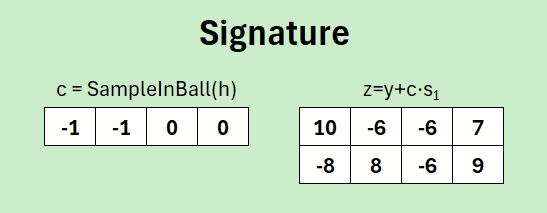
One who watches ahead will realize that in the verification a y remains permanently and is unknown. Therefore the choice of y is so difficult and may require multiple iterations: If the components of y are chosen in an unlucky way, this could either allow deductions about the private key s₁​ or lead to a verification failure. In the „real“ Dilithium a hint-vector is therefore used. This ensures that despite the unavoidable noise parts in the computation, the same HighBits can be reconstructed such that verification succeeds reliably. But first we come exactly to that: to the signature verification.

Signature Verification

Let’s first look at what we have on the receiver’s side. Here the public key (A,t) is available, the message „This is a test message“ that was signed, and of course the signature itself, consisting of (c,z).

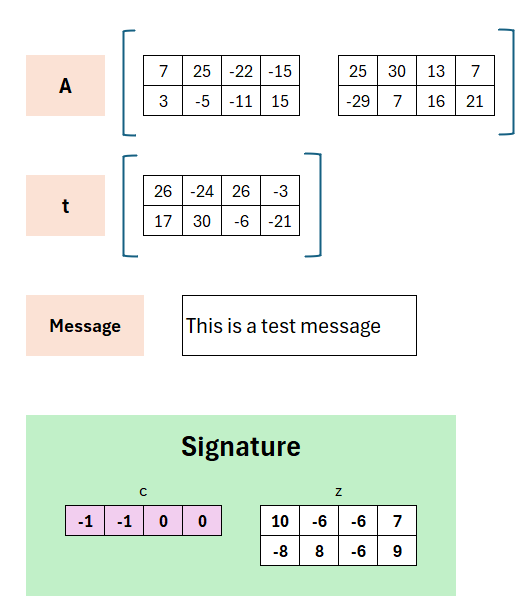
During signature verification one computes A⋅z−c⋅t. Why exactly, this can be shown later somewhat easier. At this point let’s first look at the result.

If we compare the result with our earlier A⋅y from the signature creation process …

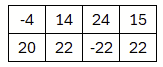
then we find that they are different. But if we look closely we might observe that the difference is not so large. The deviations are comparatively small. These would therefore rather lie in the LowBit domain. So we would hope that the HighBit domain is identical.

If we examine the HighBits then our hopes are confirmed. We get a w₁‚ which is identical to the w₁​ from signature creation. Even though we couldn’t compute y, it was chosen such that it has no effect on the HighBit domain. This w₁‚ is likewise concatenated with the message, hashed, and used as seed in the SampleInBall function.

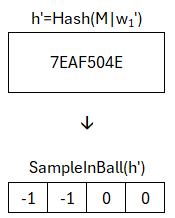
We can now check whether the output of the SampleInBall function is identical with the challenge c from the signature. This is the case. Thus the signature is successfully verified and valid. The additional check is only presented for completeness and is intended to protect against an attack with too large z.

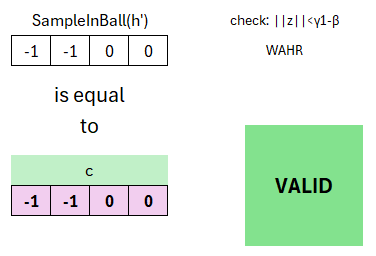
If we change the message, this leads to a different SampleInBall output and thus the signature-verification process fails.

Correctness

The correctness of the scheme is not quite easy to depict. But if we start at the verification process and keep substituting variables then in the end A⋅y−c⋅s₂​ remains.

\begin{aligned}
w_1'= Az - ct 
&= A(y + cs_1) - ct \\[6pt]
&= Ay + Acs_1 - c(As_1 + s_2) \\[6pt]
&= Ay + cAs_1 - cAs_1 - cs_2 \\[6pt]
&= Ay - cs_2 \
\end{aligned}

The original w₁​ consisted only of the product of A with y.

w_1 = Ay

For the scheme to work, the parameters are chosen such that with respect to the HighBits the same result is computed. Subsequently the same hash-value and the same result of the SampleInBall function arise.

\begin{aligned}
\mathrm{HIGHBITS}(Ay - cs_2, 2\gamma_2) = \mathrm{HIGHBITS}(Ay, 2\gamma_2) \, 
\end{aligned}

More information on correctness can be found in this document.

Excel Implementation

For demonstration of the scheme the simplified version presented here was implemented in Excel. As already explained, however, Dilithium requires the use of a hash function. For this purpose the hash function MurmurHash3 was implemented. It should be pointed out here that it is not a cryptographic hash-function; in the „real“ Dilithium SHAKE‑128/256 is used. Due to the 4-byte output length, MurmurHash3 was nevertheless suitable for this purpose. It was additionally expanded into a PRNG to generate seed-controlled random bytes.

Download of the Microsoft Excel file. Macros were omitted; due to the lambda-functions the result only works under Office 365 or Excel 2024.

_{SHA256: DE8C9D409F65C2105936D1F585BA0F5463DC67EFFFBE1B14667FC8D64E7C1EE3}

1. Actually the amount is fixed in the scheme by the Greek letter tau and hence also used here. ↩︎