SPHINCS+ bzw. SLH-DSA ist eines der PQC-Verfahren, die 2024 vom NIST standardisiert wurden. SLH-DSA wird als besonders konservative, hashbasierte Alternative zu ML-DSA gesehen, welches langfristige Sicherheit bietet und als Reserve gedacht ist, falls sich bei gitterbasierten Verfahren Schwächen zeigen

Um das Verfahren zu verstehen, sind jedoch einige Grundlagen hilfreich. Im Folgenden werden daher Lamport-OTS, Merkle-Bäume, Winternitz-OTS, HORS, HORST und FORS erläutert. Auf dieser Basis lässt sich der dem Verfahren zugrunde liegende Hypertree gut nachvollziehen.

In diesem Dokument werden Screenshots aus einer Excel-Datei verwendet, die am Ende des Dokuments bereitgestellt ist. Bitte beachten Sie, dass darin die Murmur3-Hashfunktion zum Einsatz kommt, die keine kryptografische Sicherheit bietet, für Demonstrationszwecke jedoch vollkommen genügt.

Video

Lamport-OTS

Die Lamport-Einmalsignatur (OTS) kommt in SPHINCS+ zwar nicht direkt zum Einsatz, bildet aber eine wesentliche Grundlage. Sie zeigt, wie sich allein mit einer Hashfunktion eine Signatur konstruieren lässt, die ohne Kenntnis geheimer Parameter verifiziert werden kann. Das zugrunde liegende Prinzip ist denkbar einfach.

Zur Veranschaulichung verwenden wir eine Hashfunktion mit 32 Bit Ausgabelänge; in der Praxis sind 256 Bit üblich.

Für jedes Bit des Hashwerts erzeugen wir ein Paar aus zwei unabhängigen Zufallswerten. Bei 32 Bit entstehen so 32 Paare, also insgesamt 64 Zufallswerte. Abbildung 1 (links) illustriert dies, indem die erste Gruppe von 32 Zufallswerten den Bitwert 0 und die zweite Gruppe den Bitwert 1 repräsentiert.

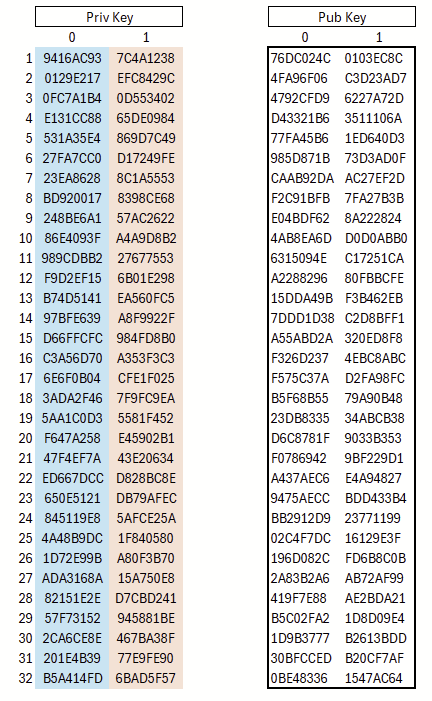
Durch einmaliges Anwenden einer Hashfunktion entsteht aus jedem Element der linken Spalte das entsprechende Element der rechten Spalte. Die insgesamt 2×32 so gewonnenen Hashwerte bilden den öffentlichen Schlüssel, der veröffentlicht werden kann. Aufgrund der Urbild-Resistenz der Hashfunktion lässt sich aus einem gegebenen Hashwert das zugehörige Urbild nicht berechnen; folglich kann aus dem öffentlichen Schlüssel kein privater Schlüssel abgeleitet werden.

Damit ist das Schlüsselmaterial erzeugt. Da es sich um ein Einmal-Signaturverfahren handelt, kann mit einem öffentlichen Schlüssel genau eine Signatur erstellt werden. Zur Signaturerzeugung wird zunächst der Hash der zu signierenden Nachricht berechnet. Die Bitfolge dieses Hashes bestimmt, welche privaten Schlüsselanteile offengelegt werden: Steht an einer Position eine 0, wird die linke Komponente des entsprechenden Paares veröffentlicht, bei einer 1 die rechte. Zur Verifikation hasht der Prüfer die offengelegten Werte und vergleicht sie mit den passenden Einträgen des öffentlichen Schlüssels (links bei 0, rechts bei 1). Stimmen alle überein, ist die Signatur gültig. Die Signaturbildung ist in Abbildung 2 dargestellt.

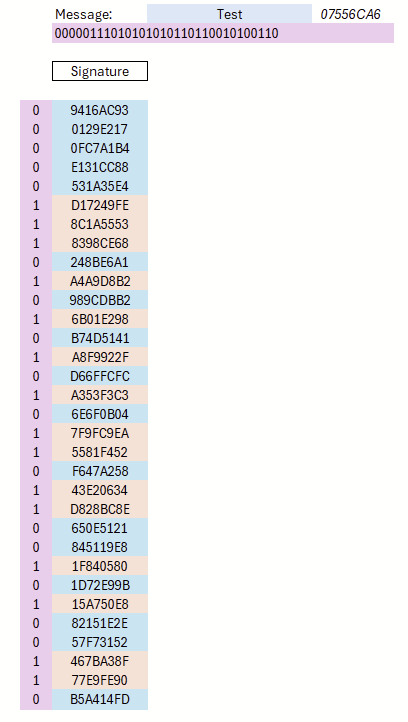
Eine offensichtliche Schwäche dieses Verfahrens besteht darin, dass der öffentliche Schlüssel ausschließlich der Verifikation einer Signatur dient. Ebenfalls nachteilig ist die vergleichsweise große Länge von öffentlichem Schlüssel und Signatur: Bei Verwendung von SHA‑256 werden dafür bereits 2×256 Hashwerte benötigt.

Merkle-Tree

Um das Problem großer öffentlicher Schlüssel zu verringern, verwendet SPHINCS+ Merkle-Bäume. Dabei werden die öffentlichen Schlüssel als Blätter eines binären Baums angeordnet; jeder innere Knoten entsteht, indem die Hashfunktion auf die Verkettung seiner beiden Kindknoten angewendet wird. Sind beispielsweise zwei Kindknoten A und B gegeben, ergibt sich der Elternknoten als H(A || B).

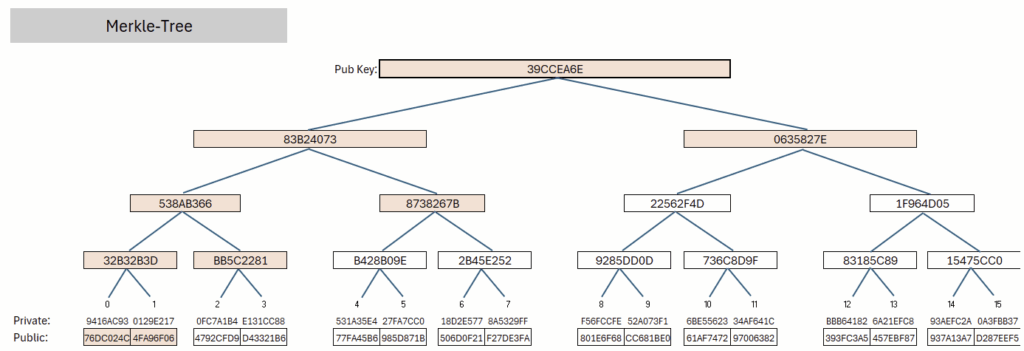
Abbildung 3 zeigt einen solchen Baum: Aus 16 zufällig gewählten privaten Werten werden mittels einer Hash-Funktion öffentliche Werte erzeugt, die die Blätter des Baums bilden. Durch die paarweise Verknüpfung benachbarter Knoten entsteht an der Wurzel ein gemeinsamer öffentlicher Schlüssel, der den gesamten Baum repräsentiert.

Um den öffentlichen Schlüssel an der Wurzel zu berechnen muss der vollständige Baum aufgebaut und durchgerechnet werden; anschließend genügt es nur einen Teil der Werte im Speicher zu behalten. Zu beachten ist, dass bei der Erzeugung der Signatur nicht alle öffentlichen Werte offengelegt werden müssen, damit der Merkle-Baum im Rahmen der Signaturvalidierung auf Richtigkeit überprüft werden kann. In Abbildung 3 ist ein Pfad von einem Blattpaar zur Wurzel markiert. Nur diese Werte sind erforderlich, um die Gültigkeit des öffentlichen Schlüssels zu überprüfen. Somit ist keine vollständige Veröffentlichung des Merkle-Baums zur Überprüfung der Signatur erforderlich, sondern lediglich der Pfad von Blatt zur Wurzel einschließlich der jeweiligen Nachbarknoten.

Winternitz-OTS

Winternitz One-Time Signatures (W-OTS) sind eine Weiterentwicklung des Lamport-Schemas und reduzieren die Anzahl benötigter Hashwerte. Das Verfahren ist jedoch etwas weniger intuitiv als das Lamport-Verfahren.

Die Kernidee: Statt jedes einzelne Bit der Nachricht separat zu signieren, fasst man jeweils zwei Werte zusammen und verarbeitet sie gemeinsam.

Beginnen wir mit einem einfachen Beispiel. Wir erzeugen einen zufälligen Startwert, etwa 9416AC93, und wenden wiederholt eine Hashfunktion darauf an:

H(9416AC93)=76DC024C
H(H(9416AC93))=H(76DC024C)=97028DBD
H(H(H(9416AC93)))=H(97028DBD)=F7E44484

Der letzte Wert dient als zugehöriger öffentlicher Schlüssel zum privaten Startwert 9416AC93. Es entsteht die Hashkette:
9416AC93 -> 76DC024C -> 97028DBD -> F7E44484

Diesen Prozess wiederholen wir für 16 unabhängige Zufallswerte. Diese 16 Startwerte bilden gemeinsam den privaten Schlüssel; die jeweiligen Endpunkte der Ketten fungieren als zugehörige Komponenten des öffentlichen Schlüssels (vgl. Abbildung 4).

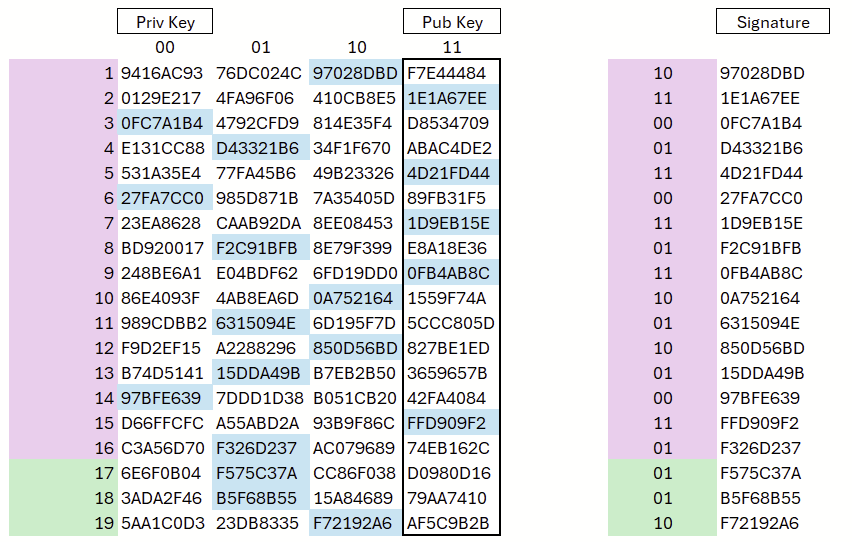
Die vier Spalten stehen für die Bit-Kombinationen 00, 01, 10 und 11. Zur Signaturbildung wird der (Hash der) Nachricht zweibitweise gelesen: Jede Zweiergruppe bestimmt die zugehörige Spalte, deren hinterlegter Hashwert offengelegt wird.

Im Beispiel beginnt die Binärdarstellung mit 10 11 00 01 110011 …; entsprechend werden der Reihe nach die Hashwerte aus Spalte 3, Spalte 4, Spalte 1 und Spalte 2 zur Signatur verwendet (vgl. Abbildung 5).

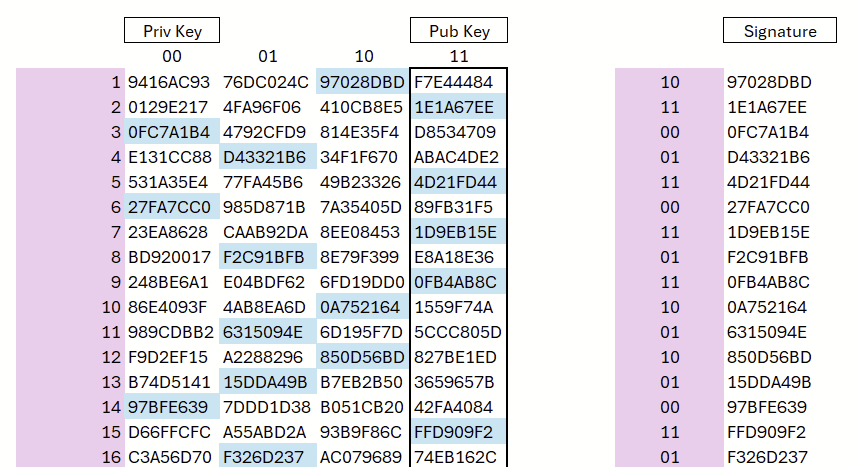
Zur Signaturprüfung wird der jeweils veröffentlichte Wert je nach Position 0 bis 3 Mal gehasht. Stimmt das Ergebnis mit dem im öffentlichen Schlüssel hinterlegten Referenzwert überein, gilt der Eintrag als gültig. Beispiel: Der veröffentlichte Wert 97028DBD (Zeile 1) wird einmal gehasht; ergibt sich dabei F7E44484, wie im öffentlichen Schlüssel angegeben, ist er korrekt.

Ohne zusätzliche Absicherung ließen sich jedoch sehr kleine Manipulationen (etwa Ein- oder Zwei-Bit-Änderungen) unbemerkt durchführen. So könnte ein Angreifer in Zeile 1 die Bits von 10 auf 11 erhöhen und den Wert 97028DBD durch den öffentlichen Schlüsselwert F7E44484 ersetzen – die Verifikation würde das nicht bemerken. Deshalb wird die Signatur um eine Checksumme ergänzt. Vereinfacht gesagt gilt: Wird ein Wert in einer Kette nach rechts verschoben, muss an anderer Stelle eine entsprechende Verschiebung nach links erfolgen. Diese Gegenverschiebung kann ein Angreifer jedoch nicht bestimmen, da ihm nur die weiter rechts liegenden Werte bekannt sind und sich die benötigten Vorstufen nicht zurückrechnen lassen. Dadurch bleiben auch Ein-Bit-Änderungen nicht unentdeckt. Abbildung 6 zeigt eine WOTS-Signatur einschließlich Checksumme.

WOTS bzw. WOTS+ wird in SPHINCS+ in der hier beschriebenen Form eingesetzt. Das Plus kennzeichnet, dass die Eingabewerte vor dem Hashen zusätzlich XOR-weise mit einer Maske kombiniert werden. Diese Technik erleichtert Sicherheitsbeweise, bleibt hier jedoch unberücksichtigt. In SPHINCS+/SLH-DSA wird ein Winternitz-Parameter w = 16 verwendet: Das entspricht 4-Bit-Blöcken (Hex-Ziffern); jede WOTS+-Kette hat somit 16 Positionen (0 bis 15).

HORS/HORST

HORS (Hash to Obtain Random Subset) und seine baumbasierte Variante HORST gelten als Vorläufer von FORS. FORS kommt in SPHINCS+ zum Einsatz, während in früheren SPHINCS-Versionen (etwa SPHINCS-256) noch HORST verwendet wurde.

Lamport-OTS und Winternitz-OTS sind echte One-Time-Signatures: Mit einem Schlüsselpaar lässt sich genau eine Signatur erstellen. HORS/HORST und FORS sind dagegen Few-Time-Signature-Verfahren. Das bedeutet, dass ein Schlüsselpaar nach der ersten Signatur nicht sofort verbraucht ist, sondern für einige wenige weitere Signaturen wiederverwendet werden kann.

Das Verfahren ist dabei vergleichsweise einfach. Zunächst werden, wie bei Lamport-OTS, eine Reihe von Zufallswerte erzeugt und mittels Hashverfahren der öffentliche Schlüssel zu jedem Wert gebildet (Abbildung 7).

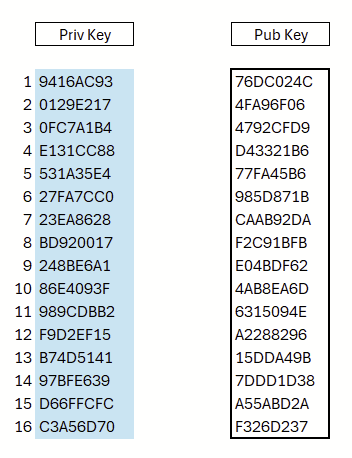
Aus dem Hash der Nachricht wird deterministisch eine kleine Teilmenge öffentlicher Hashwerte ausgewählt, die als Stichprobe dient. Zu den entsprechenden Positionen werden die jeweiligen privaten Werte offengelegt. Im gezeigten Beispiel werden stets 4 Bit der Nachricht herangezogen, um deterministisch einen privaten Schlüssel zu bestimmen; bei einer anderen Nachricht ergibt sich entsprechend eine andere Auswahl privater Schlüssel. Bei wiederholter Nutzung würden jedoch nach und nach alle privaten Schlüssel preisgegeben. Das Verfahren ist daher nicht für eine solche Mehrfachverwendung vorgesehen; es soll lediglich sicherstellen, dass eine Wiederverwendung nicht sofort katastrophale Folgen hat – anders als bei WOTS.

Der Prozess der Signaturbildung, der Erzeugung und der Wahl der Stichprobenwerte kann in Abbildung 8 nachvollzogen werden.

Kombiniert man dieses Konzept mit einem Merkle-Baum, erhält man HORST. Dabei werden die öffentlichen Schlüssel in einer Baumstruktur organisiert, sodass am Ende ein einzelner öffentlicher Schlüssel entsteht, der den gesamten Baum repräsentiert. Dass in diesem Fall die Blätter anhand der Nachricht ausgewählt werden, ist leicht nachzuvollziehen. Dies ist in Abbildung 9 dargestellt.

FORS

Auch FORS (Forest of Random Subsets) ist ein Few-Time-Signature-Verfahren. Während wir zuvor stets einen einzelnen Baum betrachtet haben – in den Abbildungen aus Darstellungsgründen klein, in der Praxis jedoch mit deutlich größerer Höhe -, setzt FORS auf mehrere kleine Bäume, also auf einen Wald. Die Nachricht wird in mehrere Teile zerlegt; jedem Baum wird genau ein Teil zugeordnet. Abhängig von diesem Nachrichtenteil wird im jeweiligen Baum deterministisch ein Blatt ausgewählt.

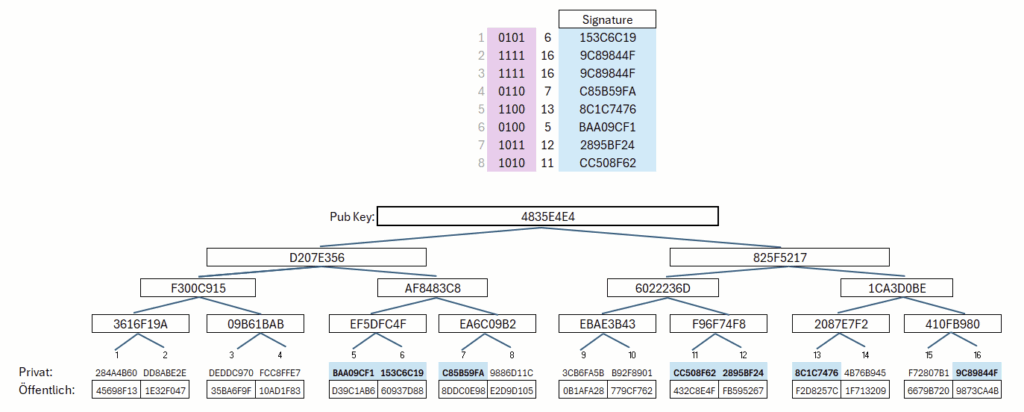
Schritt für Schritt: Betrachten wir dazu Abbildung 10. Teilen wir die Nachricht in acht Segmente, erhält jedes Segment einen 4-Bit-Wert. Diese acht Werte ordnen wir jeweils einem Baum zu und leiten aus jedem 4-Bit-Wert deterministisch das zu wählende Blatt (Leaf) ab. In diesem Beispiel berechnen wir dazu einfach (Wert modulo 4) + 1.

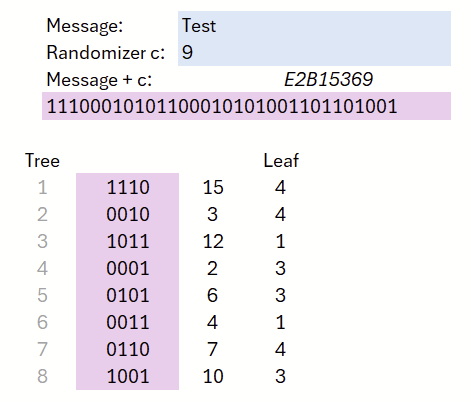
Somit ergeben sich folgende Zuordnungen: Baum 1 → Blatt 4, Baum 2 → Blatt 4, Baum 3 → Blatt 1. Jeder Baum entspricht dabei einem Merkle-Tree: Aus einer Menge geheimer (privater) Werte werden mittels eines Hashverfahrens öffentliche Werte abgeleitet und in einer Baumstruktur organisiert. Betrachten wir zunächst diese drei Bäume im Detail (Abbildung 11): In den ersten beiden Bäumen wurde jeweils das vierte Blatt ausgewählt, im dritten das erste. Für diese ausgewählten Blätter werden die zugehörigen privaten Schlüssel offengelegt.

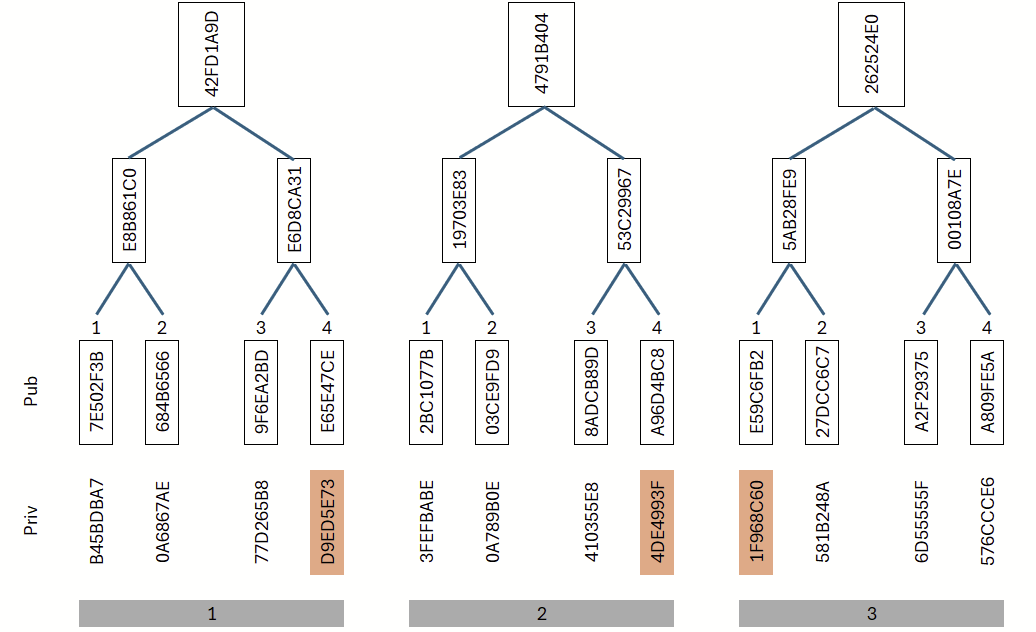
Jedem Abschnitt der Nachricht wird ein Baum zugeordnet; abhängig vom Inhalt wird jeweils ein passendes Blatt ausgewählt. Ändert sich die Nachricht, ergibt sich voraussichtlich eine andere Blattauswahl. Die acht verwendeten Bäume sind in Abbildung 12 dargestellt.

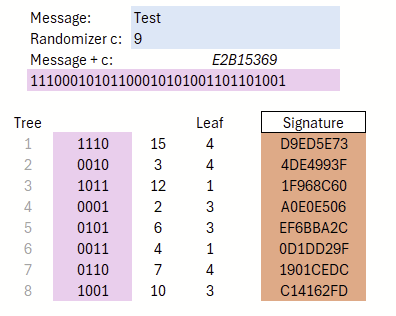
Aus der Selektion dieser Blätter ergibt sich somit die Signatur der Nachricht, die in Abbildung 13 betrachtet werden kann.

SPHINCS+

Ein Hypertree ist ein Merkle-Baum aus Merkle-Bäumen. Er ermöglicht es, sehr viele Signaturen unter einem einzigen öffentlichen Schlüssel zu authentisieren – und das zustandslos (stateless), also ohne nachhalten zu müssen, welche Blätter bereits verwendet wurden. Die Wurzeln der unteren Bäume dienen jeweils als Blätter der nächsthöheren Bäume, bis hin zur obersten Wurzel, die den öffentlichen Schlüssel bildet. Die Bäume, die untereinander verbunden werden, werden auch Layer genannt.

Wird in SPHINCS+ eine Nachricht signiert, wird abhängig vom zu signierenden Wert ein Pfad in diesem Hypertree bis zu einem Blatt ausgewählt. Dieses Blatt stellt den Übergang zu FORS dar. Die tatsächliche Signatur wird somit mit FORS vorgenommen, während die einzelnen Bäume untereinander mittels Winternitz-OTS verbunden und abgesichert sind.

Die gesamte Struktur wird deterministisch aus einem Geheimnis konstruiert. Somit ist sichergestellt, dass stets derselbe Baum erzeugt und zur Signaturbildung genutzt wird.

SHORT vs. FAST

Betrachtet man Abbildung 14 erneut, lässt sich feststellen, dass es verschiedene Möglichkeiten gibt, einen solchen Baum zu konstruieren. Mögliche Parameter sind die Höhe der Gesamtstruktur, die Höhe der einzelnen Merkle-Bäume sowie die Höhe und Anzahl der Bäume im FORS.

Um die Wurzel eines Merkle-Baums zu berechnen, muss der vollständige Baum aufgebaut werden; dabei wächst die Anzahl der Blätter exponentiell. Dies nimmt somit einige Zeit in Anspruch.

Verringern wir die Höhe der Merkle-Bäume, benötigen wir jedoch mehr davon, um eine vergleichbare Anzahl an Blättern zu erreichen. Mehr Bäume bedeuten wiederum mehr Signaturen beziehungsweise Verknüpfungen zwischen den Bäumen. Das vergrößert die Gesamtsignatur, da diese Verbindungsinformationen darin enthalten sein müssen.

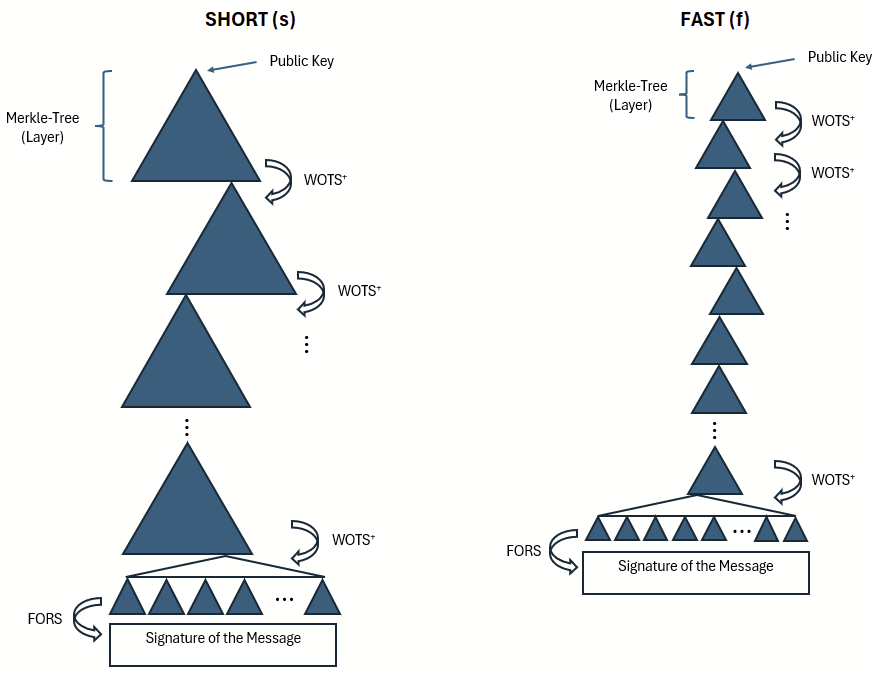
In Abbildung 15 werden SHORT und FAST einander gegenübergestellt. Größere Layer führen zu kürzeren Signaturen, erfordern dafür jedoch längere Berechnungszeiten. Kleinere Layer führen zwar zu mehr Signaturen und erhöhen damit deren Gesamtlänge, können jedoch schneller berechnet werden.

Zusammenfassung

Zum Abschluss sollen die einzelnen Puzzleteile zu einem gemeinsamen Bild zusammengefügt werden. Zur Erstellung eines öffentlichen Schlüssels ist zunächst ein geheimer Ausgangswert (Seed) erforderlich. Aus diesem Geheimnis wird deterministisch der Merkle-Baum der obersten Ebene erzeugt; seine Wurzel bildet den öffentlichen Schlüssel.

Zur Erzeugung einer Signatur wird aus der Nachricht (ggf. unter Verwendung eines Zufallswerts) ein Hashwert berechnet. Ein Teil dieses Hashwerts legt den Weg durch den Hypertree eindeutig fest. Dieser Weg erfordert den vollständigen Aufbau der jeweils benötigten Ebenen. Die Ebenen sind über WOTS+ miteinander verknüpft. Eine Signatur muss sowohl den Pfad durch jede Ebene als auch die entsprechenden WOTS+-Signaturen enthalten.

Es wird davon ausgegangen, dass jede Nachricht einen anderen Pfad im Hypertree auswählt (insgesamt gibt es etwa 2^64 Blätter), sodass die Wahrscheinlichkeit, zweimal im selben FORS-Baum zu landen, vernachlässigbar ist – zumindest bis zu einer gewissen Anzahl an Signaturen.

Auf der untersten Ebene (letzter Layer) wird für FORS ein Wald aus „kleinen“ Bäumen erzeugt. Anschließend wird der andere Teil des Hashwerts verwendet, um in FORS Bäume und Blätter auszuwählen. Für die ausgewählten Blätter werden die jeweiligen geheimen Werte offengelegt; sie dienen zusammen mit den Authentifizierungspfaden als Signatur der Nachricht.

Zur Verifikation werden in FORS die abgeleiteten Hashwerte und der öffentliche Schlüssel überprüft; anschließend verifiziert man nacheinander die WOTS+-Signaturen der einzelnen Layer, bis man die oberste Ebene erreicht. Abschließend wird geprüft, ob der öffentliche Schlüssel durch den Baum korrekt abgeleitet werden kann. Ist dies der Fall, ist die Signatur gültig.

SPHINCS+ in Excel

Die hier vorgestellten Konzepte wurden beispielhaft in Excel implementiert. In der Demo wurde aus offensichtlichen Gründen jedoch auf die Verknüpfung der Layer mittels WOTS+ verzichtet. Berechnet und dargestellt werden der Pfad durch einen Hypertree mit vier Layern sowie die Erzeugung der Signatur mittels FORS mit fünf Bäumen.

Auf Makros wurde verzichtet; aufgrund der Lambda-Funktionen wird das Ergebnis jedoch nur unter Office 365 oder Excel 2024 lauffähig sein.

_{^SHA256: 27F5F96E81C649E79B2D5BFFA95C9F6CECB73B402B85C36850854E456CFD9058}