Quantencomputer stellen bekannterweise eine Gefahr für alle asymmetrischen Verfahren dar, deren Sicherheit hauptsächlich auf modularer Arithmetik beruhen. Dies ist insbesondere bei RSA und bei Diffie-Hellman der Fall. Der Shor-Algorithmus ist ein Beispiel dafür, wie auf Basis von Quantenoperationen eine Primfaktorzerlegung durchgeführt werden kann.
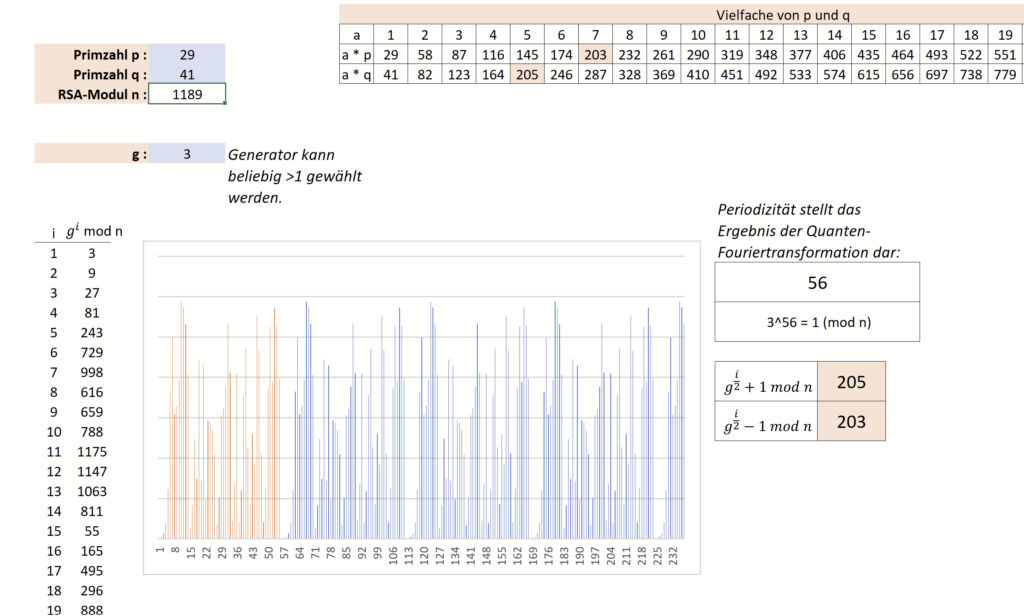
In RSA werden zwei Primzahlen miteinander multipliziert, z. B. p=29 und q=41, um ein RSA-Modul n=29*41=1189 zu bilden. Zusätzlich werden zwei Exponenten gewählt, die in einem inversen 1Verhältnis zueinander stehen um Ver- und Entschlüsselung zu ermöglichen bzw. für die Signaturerstellung und Verifizierung.
Es ist jedoch nicht so ganz einfach nachzuvollziehen, auf welche Weise Quantencomputer hier einen Vorteil erbringen. Es ist zwar korrekt, dass diese durch einen Superpositionszustand viele Berechnungen gleichzeitig durchführen. Allerdings liefert die Messung des Systems nur ein einzelnes Ergebnis. Ohne eine geschickte algorithmische Gestaltung, so wie beim Shor-Algorithmus, geht der in der Superposition enthaltene Informationsgewinn beim Messen verloren.
Der Schlüssel des Shor-Algorithmus liegt darin, mithilfe der Quanten-Fouriertransformation periodische Strukturen zu erkennen. Diese Periodizität ist direkt mit der Faktorisierung verbunden. Das ermöglicht es, die richtigen Faktoren in polynomieller Zeit zu finden – ein enormer Vorteil gegenüber der klassischen, exponentiellen Suche. Dieser Vorgang soll in diesem Artikel näher dargestellt werden.
Zunächst wird auf Basis von Quantenregistern eine modulare Exponentiation parallel durchgeführt, dass mit wenigen tausend (fehlerfreien) Registern alle möglichen Ergebnisse von g^i mod n (g beliebig gewählt) ermittelt werden können.
Schauen wir uns zunächst an, was für Ergebnisse hier produziert werden. Sei weiterhin n=1189 und g=3 (beliebig gewählt) dann erhalten wir die folgenden Ergebnisse.
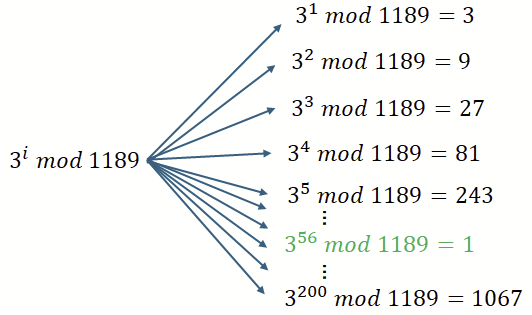
Wie leicht zu erahnen ist genau die 1 welche uns hier näher interessiert. Sie stellt das Ende einer Periode dar, die mit 3^0 = 1 beginnt. Somit wiederholen sich die Ergebnisse ab 3^56 erneut: 3^57 ist somit die 3 und 3^58 die 9 usw. Diese Periodizität lässt sich über ein Balkendiagramm leicht erfassen.
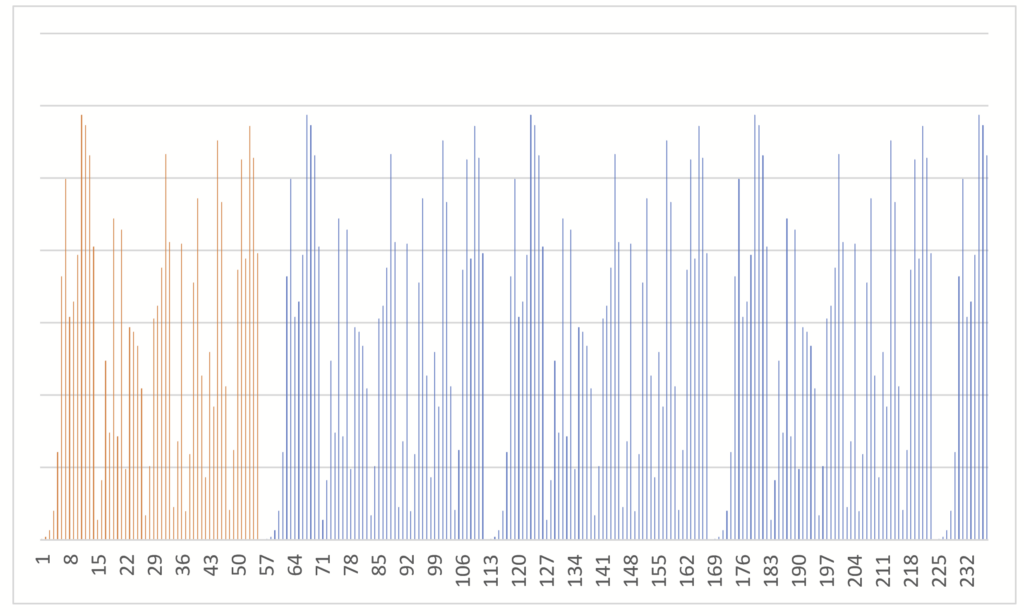
Das Balkendiagramm zeigt die Ergebnisse der 3^i mod 1189 Operation. Der orange Teil zeigt die ersten 56 Ergebnisse. Im Anschluss ist leicht ersichtlich, wie sich die Ergebnisse wiederholen. Die selben Werte kommen somit mit einer bestimmten Periodenbreite, hier 56, wiederholend vor.
Diese Periodizität lässt sich auf Basis der Quanten-Fourertransformation bestimmen. Sie stellt somit das Ergebnis der Verarbeitung auf Quantenebene dar.
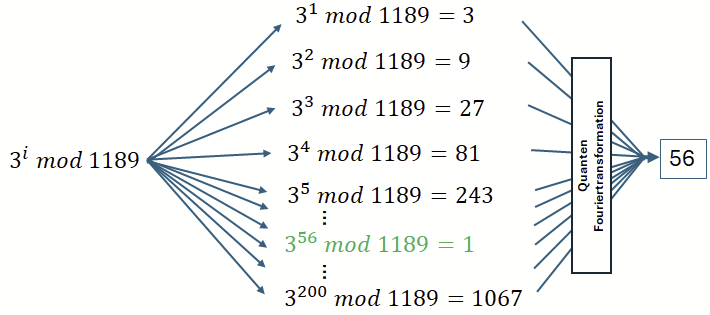
Ist diese Periodizität ermittelt, kann über einen „Trick“ eine Faktorisierung von n erreicht werden. Nehmen wir den Generator und potenzieren ihn mit der halben Periodenlänge so erhalten wir einen Wert: in diesem Fall 204.
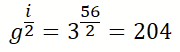
Aus der Zahlentheorie kennen wir ein Verhältnis: Dieser Wert, jeweils um eins erhöht und eins verringert, stellt ein Vielfaches mindestens einer der Primfaktoren dar. Zur Erinnerung, die Primfaktoren waren p=29 und q=41,
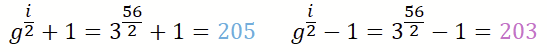
So ist 7-Mal der Faktor p die 203 und 5-Mal der Faktor q die 205. Ist der Wert erstmal errechnet, lässt sich über ein Polynomialzeit-Algorithmus der Primfaktor ermitteln: herbei hilft der Euklidischer Algorithmus.
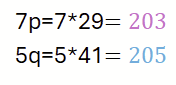
Der ggt(203,n) ist 29 und ggt(205,n) ist 41. Es ist nicht immer gegeben, dass beide Primfaktoren sich auf diese Weise ermitteln lassen. Jedoch gelingt dies mindestens für einen der Primfaktoren, womit der zweite leicht bestimmt werden kann.
Somit haben wir die Primfaktoren erfolgreich ermittelt und RSA ist gebrochen. In diesem Artikel wurde die Verarbeitung auf Quantenebene allerdings nur angedeutet. Weitere Informationen hierzu finden sich unter geeksforgeeks.org.
Um die Vorgehensweise zu visualisieren wurde der klassische Part in Microsoft Excel nachimplementiert. Hierbei kann für kleine RSA-Module die Periodizität durch klassisches Brute-Force bestimmt und die Faktorisierung nachvollzogen werden.
Download der Microsoft Excel-Datei. Auf Makros wurde verzichtet; aufgrund der Lambda-Funktionen wird das Ergebnis jedoch nur unter Office 365 oder Excel 2024 lauffähig sein.
SHA256: 246D8AC8B704BBA87D85F0B902F153710D94BD84CD5CD5B2EA5482CBFE7E9B8E
- Invers in Bezug zu phi(n) also (p-1)*(q-1). ↩︎
