Hallo liebe Gemeinde,

eine Vermutung wurde ja geäußert (siehe Kommentare). Dieser geht in die Richtung, den Klartext mit einem zufälligen Schlüssel zu chiffrieren und diesen wiederrum mit dem geheimen (ausgetauschten) zu verschlüsseln und an die Nachricht anzuhängen. Also: [E_tempkey(Text) | E_key(tempkey)]. Also ein ähnliches System wie bei den DLC-Containern.

Die Idee ist natürlich nicht schlecht, allerdings handelt es sich hierbei um etwas anderes. Und zwar gibt es in der Praxis verschiedene Betriebsmodi; um einige zu nennen: ECB, OFB, CFB. Und an dieser Stelle wurde der CBC „Cipher Block Chaining“ Modus verwendet. Was dies nun genau bedeutet ist etwas schwierig zu eklären, daher beschränke ich mich an dieser Stelle darauf den Unterschied zwischen dem simpelsten (ECB) darzustellen.

Beim ECB-Modus wird der Klartext in gleiche Stücke getrennt. Im Beitrag zur Bildverschlüsselung (http://cryptblog.de/2008/10/06/bildverschlusselung/) hatte ich dieses Verfahren bereits erläutert. Dort wurde

“Hallo, wie geht es dir  ”

in:

“Hallo, w”, “ie geht “, “es dir  ”

aufgeteilt. Jeder dieser Blöcke wird mit dem gleichen Key verschlüsselt und so erhalten wir am Ende wieder 3 Blöcke. Beispielhaft dargestellt:

“mdjwbcxg”, “ötüeoejd”, “ndkrdkdp”.

Angenommen ich ändere das „Hallo“ im Klartext in ein „Hello“, so würde sich nur der erste Block ändern, die anderen zwei blieben unberührt. Und um diesen Einfluss zu vergrößern gibt es die oben genannten Betriebsmodi. Ein Bild dazu aus Wikipedia zum CBC-Modus:

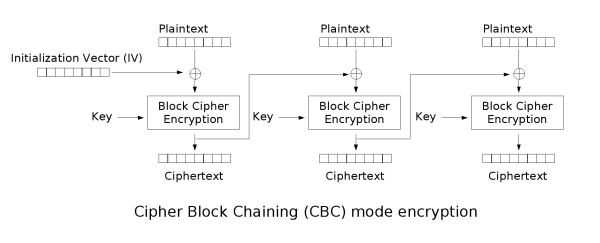
Zunächst schwierig zu verstehen. Auf der linken Seite haben wir den sehr bekannten Initialisierungsvektor. Bei der Blowfish-Implementierung wird dieser einfach zufällig gewählt. Er wird mit dem Klartext verrechnet (XOR). Das Ergebnis daraus, wird verschlüsselt und ergibt den Chiffretext welches wiederrum auf den nächsten Klartextblock Einfluss nimmt. Durch diese Pfeile ist also zu sehen, dass der Vorgänger immer auf den unmittelbaren Nachfolger einwirkt.

Dadurch ergibt sich eine Kette: wird am Anfang eine Veränderung vorgenommen, ändert dies den kompletten restlichen Chiffretext. Und da, wie schon erwähnt, der IV gewürfelt wird, ergibt sich bei jeder Verschlüsselung einen anderen Chiffretext. Zur Entschlüsselung wird allerdings dieser Vektor benötigt, daher wird er einfach mitgeschickt. Aus dem Plaintext P wird also nicht nur ein Chiffretext C, sondern beinhaltet auch einen IV.

Verstanden sollte sein, dass diese „Block für Block“-Verschlüsselung Probleme bereiten kann und ein Betriebsmodus, wie der CBC, für noch mehr Einflussnahme des Klartextes sorgt.