Hallo zusammen,
vor kurzem hatten ein Kommilitone und ich ein Problem. Wir wollten (über das Internet) ausknobeln, wer von uns mit dem Auto fahren muss und wer dafür Alkohol trinken kann. Ein Schnick-Schnack-Schnuck über das Internet sozusagen. Beide hatten wir nach einer Lösung für dieses Problem gesucht jedoch keine wirklich gute gefunden. Zuletzt entschieden wir uns dazu, es über die Anzahl der Heise.de-News des nächsten Tages zu bestimmen. Je nachdem ob es eine gerade oder ungerade Anzahl ist, muss der eine oder der andere.
Die Frage ist also, ob es dafür bessere Lösungen gibt. Mit Hilfe einer dritten, unabhängigen Instanz sollte dies nicht so schwierig sein, einige Lösungsbeispiele habe ich dafür mal ausgearbeitet:
Beide Parteien könnten mit einem Client auf einen Server verbinden. Sobald alle verbunden sind, gibt dieser eine zufällige Zahl aus. So hat man, synchronisiert, allen Teilnehmern dieses Ereignis zugänglich gemacht.
Oder man könnte eine Webseite bereitstellen, die alle 5 Minuten eine zufällige Zahl ausgibt. So könnten beide Parteien Vermutungen über die nächste Ausgabe treffen und diesbezüglich eine Entscheidung finden. Um dieses Beispiel zu verdeutlichen habe ich diese Webseite angefertigt: http://www.cryptblog.de/random.php.
Eine weitere Möglichkeit wären Kryptogramme eines Servers: Partei A bezieht ein aktuelles Kryptogramm von einem Server, welches eine verschlüsselte Zahl enthält. Er übergibt das Kryptogramm der Partei B und beide einigen sich darauf, welche Entscheidung bei einer geraden/ungeraden getroffen wird. Die Entschlüsselung ist allerdings erst später (~5 Minuten) möglich. Ich denke allerdings, dass diese Lösung unnötig kompliziert ist und kaum einen Vorteil gegenüber den anderen besitzt.
Aber nun die Frage: ist es möglich eine solche Entscheidung zu treffen, ohne dass ein Dritter (Server) beteiligt ist? Meine Antwort darauf ist JA. Folgendes Verfahren habe ich mir überlegt:
Sowohl A, als auch B, denken sich eine möglichst große zufällige Zahl (a und b) aus. Mit Hilfe einer Webseite, die hier lediglich als „Taschenrechner“ dient, berechnen A und B jeweils einen Hash (Fingerabdruck, beispielsweise MD5) ihrer Zahl, also z.B. H(a) und H(b). Über ein beliebiges Kommunikationsmedium kann nun dieser Hashwert ausgetauscht werden. Außerdem müssen sich A und B jeweils für eine gerade oder ungerade Zahl entscheiden. Durch diesen Austausch, haben sich beide auch damit einverstanden erklärt, dieses Verfahren zu nutzen. Nachdem also Hashwerte ausgetauscht sind, ist jeder im Besitz seiner eigenen Zahl und einem Fingerabdruck der Zahl des anderen.
Jetzt kann jeder seine Zahl dem anderen nennen, ob nun A oder B zuerst ist egal. Beide Zahlen werden miteinander addiert, also m = a + b berechnet, und je nachdem ob diese Zahl gerade oder ungerade ist, fällt die Entscheidung für A oder B aus. Aufgrund des vorherigen Austausch der Hashwerte, ist ein nachträgliches ändern der Zahl nicht möglich bzw. A und B können die Aussagen des anderen verifizieren.
Um dieses Beispiel zu verdeutlichen, existiert eine neue Sektion und ein Script um die Durchführung zu vereinfachen: http://cryptblog.de/muenzwurf/.
Nochmal grob zusammengefasst:
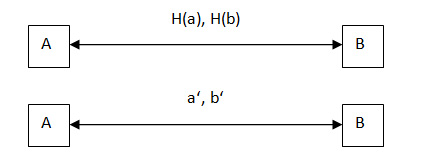
A prüft H(b)=H(b‘), B prüft H(a)=H(a‘). Sofern beides wahr, kann von a’=a und b’=b ausgegangen werden.
Beide berechnen m = a+b.
Mittels diesem Protokoll hat jeder Teilnehmer eine 50% Chance zu gewinnen:
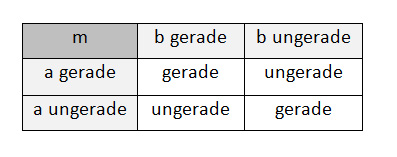
In der Anwendung ist folgendes zu beachten:
Die Hashfunktion sollte einigermaßen sicher sein und um Rainbowtables entgegenzuwirken, sollten die Zahlen möglichst groß sein. Sofern dies erfüllt ist, können auch JavaScript Lösungen zum berechnen verwendet werden, wie z.B. http://aktuell.de.selfhtml.org/artikel/javascript/md5/ .
Nachtrag:
Grundsätzlich kann man dieses System auch, leicht modifiziert, für das bekannte Stein-Schere-Papier einsetzen, indem ein Hash von Stein|Zufallszahl, Schere|Zufallszahl oder Papier|Zufallszahl gebildet und später ausgetauscht wird. Das macht die vorherige Absprache ob gerade oder ungerade unnötig.

Schreibe einen Kommentar