INFSEC.de

Kategorie: Kryptographie

  • Unsicher ist Unsicher

    Hallo zusammen,

    über Facebook bin ich auf einen Wettbewerb gestoßen, den ich euch nicht vorenthalten möchte:

    Deine Aufgabe ist es, ein Programm zu realisieren, mit dessen Hilfe es möglich ist, ausgewählte Dateien (und Verzeichnisse?) zu verschlüsseln und später wieder zu entschlüsseln.

    […]

    • Verschlüsselung von Daten über die Konsole oder ein GUI
    • Implementierung eines Verschlüsselungsalgorithmus (gerne auch ein eigens entwickelter Algorithmus!)
    • Entschlüsselung der Daten über gleiches Programm

    […]

    Quelle: Code Competition: Sicher ist Sicher. https://www.it-talents.de/cms/aktionen/code-competition/code-competition-04-2016

    Bereits in den Kommentaren auf Facebook wurde dem Betreiber von dieser Idee abgeraten. Verschlüsselungsverfahren sollten nur von dafür qualifizierten Personen konzipiert werden. Fehler können bei der Anwendung selbiger ohnehin noch genug gemacht werden. Natürlich ist es eine gute Sache, junge Menschen für die Programmierung zu begeistern. Allerdings werden auf diese Weise die Security Audit Findings von morgen generiert. Ich stelle mir das in 5-7 Jahren so vor:

    Chef: Wir brauchen in unserer Software dringend noch eine Verschlüsselungslösung um die sensiblen Daten der Kunden zu schützen.
    Talentierter Mitarbeiter: Ich habe da im Studium mal etwas gebaut, ist aber vermutlich nicht ganz si…
    Chef: Perfekt!

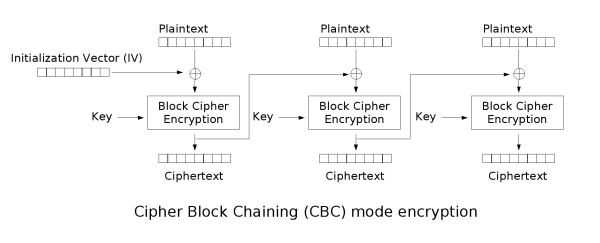
    Trotzdem hat mich dieser Ausschreibungstext inspiriert, was man wohl alles an „billigen Lösungen“ einreichen könnte, um die 222 € zu gewinnen (oder den Raspberry Pi 3). Mal von einfachen Substitutions- und Permutationslösungen abgesehen, könnte man sich einfach einer Feistelchiffren-Konstruktion bedienen (wie in DES/3DES oder Blowfish). Es hat den Vorteil, dass man sich über die Entschlüsselung keine Gedanken machen muss.

    Noch einfacher wäre es, eine Stromchiffre zu konstruieren. Für den Schlüsselstrom könnte man einfach einen PRNG (Pseudozufallsgenerator) mit einem Seed initialisieren und auf den Klartext auf-XOR-en. Das wäre nur eine Zeile – und sogar die gleiche für Ver- und Entschlüsselung.  Das fiese daran ist, dass das Ergebnis recht zufällig aussieht und ein Blackbox-Audit vermutlich sogar bestehen würde. Hier exemplarisch in Python und nur für Text, aber das geht mit einer Datei natürlich genauso gut:

    >>> import random

>>> text = "hier kann ein beliebig langer Klartext geschrieben werden"

### Verschlüsselung ###
>>> random.seed("hier den Schlüssel!"); text="".join([chr(ord(e)^random.getrandbits(8)) for e in text])
>>> text
'\xeb\xbdP~0v\xa3\xb8[c\x0f\xb7\xaa\xbe\xaf\x1f\x15#\xd2:\x17\xbeU\xfesJ\x1d\x18\xcbmb\xe256*\x9ct\xc2\rl0\xbb\x9e\xbc0GV\xc5\xadG\xa89\xa0_"\x9f\xaa'

### Entschlüsselung ###
>>> random.seed("hier den Schlüssel!"); text="".join([chr(ord(e)^random.getrandbits(8)) for e in text])
>>> text
'hier kann ein beliebig langer Klartext geschrieben werden'

    Anstelle des PRNG könnte man auch ein Hash-Verfahren nehmen und mit einem Schlüssel initiieren. Sicher ist daran jedoch nur das Lachen der Auditoren.

    Mich würden die Einreichungen sehr interessieren. Vermutlich wird am Ende die ausgefallenste Lösung gewinnen und die Sicherheit eher auf der Strecke bleiben.

     

  • Von Kühen zu Turing

    Hallo zusammen,

    heute möchte ich präsentieren, welche „Alltagsprobleme“ sich in der Kryptologie wiederfinden.

    Vor kurzem hat mich jemand angeschrieben, er säße vor einem kleinen mathematischen Problem. In seinem Dorf ist ein so genanntes Kuhfladen-Bingo geplant. Dafür muss ein Feld von fester Größe, in eine dynamische Anzahl kleinerer unterteilt werden. Nochmal langsam:

    Wir haben zunächst das große Feld bzw. die Wiese. Diese hat eine konstante Größe bzw. im Falle, dass sie rechteckig ist, eine Länge und eine Breite. Jetzt haben wir x Lose verkauft und wollen dieses Feld in x-viele gleichgroße „kleine“ Felder aufteilen. Die Summe aller kleinen Flächen entspricht der Gesamtgröße – also wir wollen stets einen Gewinner und keine „unbesetzten“ Felder. Es soll also ein Schachbrettmuster auf dieses Feld gelegt werden, wobei in diesem Fall die kleinen Felder nicht quadratisch sein müssen.

    Mathematisch ausgedrückt, suchen wir zwei ganzzahlige n und m, wobei n*m = x und x die Anzahl der verkauften Lose ist. Kennen wir n und m, können wir die Länge bzw. Breites des Feldes durch n bzw. m teilen und erhalten die Größe der „kleinen“ Rechtecke. Ein Beispiel:

    Das Feld ist L=8 x B=16 Meter groß. Es wurden zufällig 1024 Lose verkauft. Also suchen wir:

    n * m = 1024

    Eine Lösung ist: n = 4, m=256. Demnach teilen wir die Länge L=8m durch 4 und erhalten l=2m – außerdem die Breite B=16m durch 256 und erhalten b=0,0625m. Ein kleines Feld hat also die Ausmaße l=4m und b=6,25cm. Wie wir allerdings schnell erkennen, gibt es bei dieser Gleichung mehrere Lösungen. Ebenso wären n=8, m=128 und sogar die triviale Lösung n=1 und m=1024 in der Lösungsmenge enthalten.

    Einen naiven Lösungsalgorithmus finden wir also schnell: wir suchen einen Teiler von x im Intervall [2, sqrt(x)] also zwischen 2 und der Wurzel von x. Bei x=1024 ist das die 2, die 4, die 8, die 16 und die 32. Das lässt sich relativ einfach mit einer Schleife realisieren.

    Daraufhin ergab sich die Frage, ob dafür nicht auch eine bessere bzw. effizientere Lösung existiert. Das Beste wäre eine Formel, in welcher nur die Variablen einzutragen sind und dann ein brauchbares (nichttriviales) Ergebnis präsentiert. An dieser Stelle möchte ich dem Leser Zeit geben um darüber nachzudenken. Auch bezüglich der Frage, warum sich dieses Problem in einem Blog über Kryptologie wiederfindet.

    ~

    Ich habe eben gezeigt, dass wir bei diesem Problem zwei ganzzahlige Teiler suchen: n und m bzw. n*m=x. Ich ändere nun mal die Namen der Variablen: p*q=m. Sei also m ein RSA-Modul, also das Produkt zweier Primzahlen, so sind p und q ganzzahlige Teiler von m. Wir haben also „mehr oder weniger“ nach einem effizienten Algorithmus bzw. einer Formel gesucht, die RSA-Verschlüsselung zu brechen. Wären wir an jenem Abend erfolgreich gewesen, würde ich diesen Blogeintrag an einem Strand in der Karibik zu Ende schreiben.

    Wie schon oft erwähnt, ist die „schwierige“ Suche nach den Primzahlen p und q genau das, was die RSA-Verschlüsselung ausmacht. Und die Tatsache, dass für p*q=m (p,q prim) bisher noch kein effizienter Algorithmus gefunden wurde, bietet uns Schutz bei Online Banking, Zertifikaten (PKI), VPN-Tunneln und vielem mehr.

    Moooooooment. Da steht doch p*q=m (p,q prim) – also wir suchen zwei Primzahlen dessen Produkt m ergibt. Bei unserem Problem oben war jedoch die Rede von einem beliebigen Teiler! Stimmt. Es folgt ein Ausflug in die Zahlentheorie und theoretische Informatik.

    Angenommen wir hätten das oben beschriebene Feldaufteilungsproblem effizient gelöst, dann wären wir im Besitz einer Formel oder eines Algorithmus, den wir einfach F nennen – F für Feld. Wir übergeben dem Algorithmus F also die Anzahl der Lose und selbiges generiert uns zwei ganzzahlige Teiler n und m. Auf der anderen Seite haben wir das RSA-Problem – wir besitzen also einen „langsamen“ Algorithmus für dieses Problem und nennen diesen R. Wir übergeben R ein RSA-Modul (also das Produkt zweier Primzahlen) und es liefert uns das entsprechende p und q.

    Damit sind F und R also informell definiert. Nun übergeben wir, nur aus Spaß, unserem Feldproblem F ein RSA-Modul, sagen wir r(=p*q). Warum auch nicht – es ist ja auch nur eine Zahl. F liefert uns nun also zwei ganzzahlige Teiler n und m wobei gilt: n*m=r. Jetzt wird’s spannend: nach dem Fundamentalsatz der Arithmetik ist die Primfaktorzerlegung eindeutig und stets existent. D.h. das, was wir hier zurückbekommen, müssen p und q sein. Warum? Angenommen es gäbe noch eine andere Aufteilung z.B. a*b=r, dann hätte sowohl a, als auch b eine Primfaktorzerlegung (Existenz!) welche nicht mit p*q übereinstimmt. Das ist ein Widerspruch zur Eindeutigkeit – somit haben wir indirekt p=n und m=q bewiesen. #

    Dieser Teil muss nun nicht unbedingt verstanden worden sein. Wichtig ist nur, dass wir das Problem R, also die Zerlegung eines RSA-Moduls, mit Hilfe von F lösen können. In der Informatik spricht man hier auch von Turingreduzierbarkeit. Wenn wir wissen, dass wir R mittels F lösen können, dann muss R „leichter“ sein als F, bzw. „R ist turingreduzierbar auf F“ oder „F ist Orakel für R“. So lassen sich Probleme in Klassen einteilen, was relativ komfortabel ist: sobald wir einen guten Algorithmus für F gefunden haben, ist auch effizient R gelöst. So müssen wir also nur nach einer Lösung für F suchen, wobei diese auch schwieriger sein könnte als R. Äquivalenz liegt vor, wenn eine Reduktion in beiden Richtungen möglich ist. Um die Frage vorweg zu nehmen: dies ist hier der Fall; F und R sind Turing-Äquivalent (ohne Beweis).

    So sind wir von den Kühen, über die Kryptologie, zur theoretischen Informatik gekommen.

  • Sicherheit beim Online-Poker

    Hallo zusammen,

    erneut ein Problem, erneut eine Lösung.

    Bei einem Online-Poker Spiel (PokerTH, ein Open-Source-Projekt unter GPL) habe ich mir die Frage gestellt, wie fair so ein System überhaupt sein kann, unabhängig von der zugrunde liegenden Netzstruktur (P2P, Client/Server).

    Das ist meiner Meinung nach eine sehr wichtige Frage, da der Einsatz, anders als in meinem Fall, auch Echtgeld sein könnte. Nehmen wir an, der Server (bzw. der Betreiber) würfelt die Karten und übermittelt sie den Teilnehmern. Dann muss dieser auch absolut vertrauenswürdig sein. An dieser Stelle entscheidet ganz allein die Serverapplikation über Sieg oder Niederlage der Spieler – zumindest bei reinen Glücksspielen. Hier hätte jemand mit Serverzugriff gleichzeitig Einblick in alle Karten. Böswillig könnte man sogar unterstellen, der Betreiber nimmt selbst am Spiel teil und nutzt diese Kenntnis aus – ein solches Spiel kann nicht gewonnen werden. In einem Netzwerk von gleichberechtigten, also ein P2P-Netzwerk, existiert dagegen kein Host, daher müsste ein LEA (Leader Election Algorithm) entscheiden, wer die Spielrunde leitet. Das Problem bleibt jedoch bestehen: ein Teilnehmer der Runde besitzt die Möglichkeit das Spiel zu manipulieren.

    Die andere Seite ist jedoch genauso kritisch. Würfelt der Teilnehmer/Spieler die eigenen Karten, ist dies ganz offensichtlich (insbesondere bei einem Open Source Projekt), keine gute Idee. Eine weitere Möglichkeit wäre, dass ein Teilnehmer die Karten des unmittelbaren Banknachbarn bestimmt, aber von Fairness kann hier auch kaum gesprochen werden.

    Beide Lösungen sind nicht wirklich überzeugend und bedeuten stets, dass mindestens einer einen Vorteil erhält. Letztenendes besteht das Problem, dass alle Teilnehmer gemeinsam etwas bestimmen müssen, also wer welche Karten bekommt, ohne diese konkret zu erfahren. Gibt es dazu eine Lösung? Die Antwort lautet: ja.

    Aber leider nicht von mir, sondern von Adi Shamir, Ron Rivest und Len Adleman – den Entwicklern der RSA Verschlüsselung. Es handelt sich um ein Protokoll für ein faires Pokerspiel, welches hier zu finden ist. Bevor ich nun die Algorithmus skizziere, möchte ich allerdings noch erklären was eine kommutative Chiffre ist. Normalerweise muss beim Ver- und Entschlüsseln eine Reihenfolge eingehalten werden, z.B.:

    D_key1(E_key1(x))

    und

    D_key1(D_key2(E_key2(E_key1(x))))

    also sozusagen wie bei einer Zwiebel: jede Schale muss sauber und nacheinander aufgetragen und wieder entfernt werden um an den Inhalt zu gelangen. Bei einer Kommutativen Chiffre ist diese Reihenfolge irrelevant – funktionieren würde also ebenso:

    D_key2(D_key1(E_key2(E_key1(x))))

    Also: die Reihenfolge der Entschlüsselung spielt keine Rolle. Diese Eigenschaft wird beim folgenden Pokerprotokoll ausgenutzt, wobei es in der Praxis effektiv keine Einschränkung darstellt:

    1. Parteien A und B einigen sich bezüglich einer klaren Kodierung der Spielkarten.
    2. Die Partei A wählt einen beliebigen geheimen Schlüssel und verschlüsselt jede Karte einzeln.
    3. Partei A mischt die Karten
    4. Partei A übermittelt die neuen (verschlüsselten und gemischten) Karten der Partei B; B weiß daher nicht, welche Karten sich wo befinden.
    5. B verschlüsselt ebenso jede Karte mit einem Schlüssel -> jede Karte ist nun sowohl von A als auch von B mit jeweils einem Schlüssel verschlüsselt worden.
    6. B mischt die Karten.
    7. B übermittelt die doppelt verschlüsselten und gemischten Karten der Partei A.
    8. A entschlüsselt alle Karten mit seinem Schlüssel (hier tritt die Kommutativität hervor).
    9. A verschlüsselt nun jede Karte einzeln, mit jeweils einem anderen Schlüssel. Die Karten sind nun alle mit einem Schlüssel von B verschlüsselt, sowie jede einzelne mit einem jeweils anderen Schlüssel von A.
    10. A übermittelt B die neuen Karten.
    11. B entfernt seine alte Verschlüsselung (erneut die Kommutativität).
    12. B verschlüsselt, genau wie A, jede Karte mit einem eigenen und anderen Schlüssel.
    13. B übergibt A die verschlüsselten Karten.
    14. A legt die Karten für alle Teilnehmer (hier 2) offen.

    Was liegt nun vor? Die Karten wurden alle gemischt und doppelt verschlüsselt – jeweils mit einem anderen Schlüssel von A und  B. Die Karten liegen nun „auf dem Tisch“ und die Teilnehmer einigen sich darüber, wer welche Karten bekommt. Werden die ersten 5 Karten A zugeteilt, teilt B die dafür notwendigen Schlüssel mit, und umgekehrt. Jeder besitzt also nun Karten aus diesem Kartenpool die nur dem Spieler selbst bekannt sind. Ein grundsätzlich sehr solides Verfahren. Insbesondere ist es relativ intuitiv, da in der ersten Runde die Karten lediglich verdeckt gemischt werden und in der zweiten Runde dafür gesorgt wird, dass niemand die gemischten Karten „einsehen“ kann.

    Wie schon erwähnt, muss hier zwar keine asymmetrische, jedoch eine kommutative Chiffre verwendet werden. In der oben genannten Quelle wird erklärt, dass ein XOR hier nicht genügt. Wie jedes Protokoll/Verfahren hat auch dieses Schwachstellen, welche sich allerdings beheben lassen und eventuell in einem eigenen Beitrag behandelt werden.

    Ob nun die oben genannte Open Source Software diese Verfahren einsetzt, kann ich nicht beantworten – vielleicht irgendein anderer interessierter Leser. Grundsätzlich besteht jedoch die Möglichkeit solch ein Pokerspiel durchzuführen – unter Umständen wesentlich sicherer als in den Spielcasinos.

  • Primfaktorzerlegung und NP

    Hallo,

    zunächst eine Warnung: dieser Beitrag ist relativ schwierig und ohne Vorkenntnisse in theoretischer Informatik nicht zu verstehen.

    Im Laufe einer Lehrveranstaltung hat sich die Frage gestellt, ob die Primfaktorzerlegung (genauer: RSA – also 2 Primfaktoren) in NP liegt bzw. sogar NP-vollständig ist – ums populärer auszudrücken: wie viel Ärger bekommen wir, falls P=NP gilt.

    Wir haben allerdings an dieser Stelle jedoch das Problem, dass die Komplexitätsklasse NP bzw. die Laufzeitfunktion NTIME auf Sprachprobleme – also Entscheidungen definiert ist. Innerhalb der Literatur finden sich wenig und vor allem sehr oberflächliche Aussagen darüber („es ist leicht einzusehen dass dieses Problem in NP liegt…“). Die letzten Wochen habe ich intensiver darüber nachgedacht und ich denke, eine brauchbare Lösung anbieten zu können.

    Zunächst wichtige Vorarbeit:  die Frage, ob eine natürliche Zahl eine Primzahl ist oder nicht, liegt in P (also deterministischer Polynomialzeit). Erreicht wird dies durch den AKS-Primzahltest. Damit ist auch die Frage, ob eine Zahl n (ungleich 1) Primteiler besitzt in P feststellbar, da dies immer der Fall ist, sofern es sich um keine Primzahl handelt (Hauptsatz der Zahlentheorie).

    Im nächsten Schritt prüfen wir, ob die Zerlegung des RSA-Moduls in NP liegt.

    Nichtdeterministische ZerlegungNehmen wir hierzu beispielhaft die Primzahlen p=7 und q=11 also M=p*q = 7*11=77, binär dargestellt 1001101. Mittels eines naiven Nichtdeterministischen Algorithmus, können wir von 1 bis sqrt(M) alle möglichen Teiler durchprobieren. Dass dies in NP liegt, soll mittels der Abbildung gezeigt werden. Die Baumtiefe entspricht n/2, also die halbe Eingabelänge n(=7). Der Übersicht halber hier nur die Tiefe 3 anstelle 4.

    Durch diese Verzweigung erhalten wir also alle Lösungskandidaten h.

    Im blauen Kasten prüfen wir nun, ob h ein Primteiler von M ist. Sowohl der Primzahltest „ist h eine Primzahl?“ liegt in P (wie oben erwähnt), als auch die Division „ist h ein Teiler von M“. Auch würde der Primzahltest des zweiten Divisors in P liegen. Dementsprechend liefert der skizzierte Nichtdeterministische Algorithmus am Ende ein „ja“, da 111 (=7) sowohl Primzahl, als auch Teiler von M (77) ist.

    Wir haben also nun festgestellt, dass die Frage nach der Primfaktorzerlegung in NP liegt. Das hilft uns allerdings nur bedingt, da diese Antwort schon vorher bekannt war. Per Definition besitzt ein RSA-Modul zwei Primteiler, daher würde der Algorithmus natürlich stets ein ja liefern. Wir müssen also dieses Entscheidungsproblem (1)  nutzen, um effizient das Optimierungsproblem (2) zu lösen.

    Aus diesem Grund definieren also das Problem in folgender Weise neu:

    Eingabe: (M,k) wobei m das RSA-Modul (bestehen aus dem Produkt zweier Primzahlen), und k eine beliebige Zahl k<=M.

    Zulässige Lösung: ja/nein

    Frage: liegt ein Primfaktor des RSA-Moduls M unterhalb von k.

    Wir übergeben also das Modul M=(p*q) und fragen, ob sich der kleinere Primfaktor unterhalb von k befindet. Dieses Entscheidungsproblem ändert am oben skizzierten Algorithmus die Laufzeit nur um einen konstanten Faktor, welche in der polynomiellen Unschärfe sowieso verschwindet. Wir sind inder Lage, wie in der nächsten Abbildung zu sehen, mittels einer binären Suche den Primfaktor exakt zu bestimmen:


    Binäre Suche nach dem Primfaktor

    Können wir also das Entscheidungsproblem (1) als Orakel verwenden, so lässt sich auch dieses Optimierungsproblem (2) sehr effizient (logarithmisch) lösen. Die binäre Suche geht in der polynomiellen Unschärfe verloren, womit wir informell bewiesen haben: bei P=NP liegt die Faktorisierung auch in P.

    Welche Auswirkungen hätte P=NP auf den Alltag? Diese Frage lässt sich leider nicht beantworten, da nicht jeder Algorithmus in P auch effizient ist. Wäre der Exponent jedoch niedrig, wären die Folgen schwerwiegend: die PKI würde zusammenbrechen, wodurch sicheres Online Banking unmöglich wäre. Jedes asymmetrische und damit auch jedes hybride Verschlüsselungssystem wäre hinfällig. Die Quantenkryptographie, die hiervon nicht betroffen wäre, liefert keinen adäquaten Ersatz.

    Hoffen wir also, dass P != NP gilt.

  • Peer to Peer – Sicherheit

    Hallo zusammen,

    vor Kurzem ist in einem Spieleforum die Frage aufgekommen, wie es mit der Sicherheit von Peer-to-Peer Systemen aussieht. Vermutlich werden jetzt viele Leser an die juristischen Folgen durch, populär ausgedrückt, „illegale Downloads“ denken. Damit soll sich dieser Beitrag allerdings nicht befassen. Außerdem muss auch die Frage geklärt werden, wieso sich ein „Spieler“, eine möglicherweise leicht Klieschee behaftete Gruppe, dafür interessiert.

    Insbesondere MMORPGs zeichnen sich durch einen sehr dynamischen Inhalt aus, was für viele einen Reiz darstellt, eine beachtliche Menge an Zeit zu investieren. Dies erfordert jedoch einen permanenten Aktualisierungsvorgang aller Clients. Viele „Kleinigkeiten“, wie Art/Position/Verhalten von s.g. NPCs können durchaus „on the fly“ dem Spieler mitgeteilt werden. Umfangreichere Änderungen, insbesondere neue Grafiken, erfordern jedoch eine Änderung des Programms bzw. der verwendeten Bibliotheken. Hiervon soll allerdings der Spieler möglichst wenig betroffen sein – insbesondere soll er nicht gezwungen sein auf dubiosen Webseiten die Patches zu laden und dann auf dem jeweiligen Rechner zu installieren. Jedoch ein Client-Server Modell, bei dem ein Server die Daten für alle Clients bereitstellt, ist nur für geringe Benutzerzahlen praktikabel. So bedeutet ein 100 MB Update, was durchaus nicht selten ist, bei 100.000 Spielern nunmal 10.000.000 MB Traffic, also 10 TB. An dieser Stelle sei noch anzumerken, dass es durchaus Spiele mit 5-10 Millionen aktiven Spieler gibt. Außerdem besteht ein betriebswirtschaftliches Interesse, die Kosten solcher Prozesse möglichst gering zu halten.

    Was also tun? Das Thema liefert die Antwort: Peer to Peer Netzwerke, kurz P2P. Wie funktioniert das?
    Nunja, viele leichtverständliche Informationen findet man auf einschlägigen Webseiten. Ich möchte an dieser Stelle insbesondere auf das P2P Netz eingehen, welches überwiegend beim Filesharing eingesetzt wird. Auch wenn „Filesharing“, „Peer to Peer“, etc. vielen Lesern die roten Alarmglocken schlagen lässt: es ist eine Technik, die von vielen Unternehmen eingesetzt wird und daran ist überhaupt nichts Illegal. Sie eignet sich allerdings auch zum Tausch von geschütztem Material wodurch sie häufig in einen falschen Zusammenhang gesetzt wird. Um dieses System in kurzen Worten zu erklären, möchte ich mich der Schneeball-Metapher bedienen:

    Durch umfangreiche Aufklärungsarbeit der öffentlich rechtlichen Funk und Fernsehanstalten sollte vielen Lesern bekannt sein, wie ein Schneeballsystem (oder ein Kettenbrief) funktioniert. Wir definieren eine Person, die ein Produkt an eine Reihe von Personen anbietet und nennen diesen Tracker. Diese Reihe von Personen bemühen sich, aus eigenem Interesse, möglichst viele weitere Personen für dieses Produkt zu gewinnen. Wir bezeichnen alle Personen, die daran interessiert sind, als Schwarm. Angenommen jeder Teilnehmer gibt das Produkt (oder die Information) nur an zwei Andere weiter, haben wir nach 30 Schritten schon eine Schwarmgröße von 1.073.741.823 (2^30-1). Der Aufwand für den Einzelnen, 2 weitere zu „finden“ bzw. zu bedienen, war relativ gering – in der Gesamtheit war das Produkt jedoch ein riesen Erfolg.

    Als Informatiker möchte ich jedoch an dieser Stelle anmerken, dass es sich hierbei um einen Baum der Ordnung 2 handelt – hingegen ein P2P System als ein Multigraph anzusehen ist. Übertragen auf das „Updateproblem“: der Tracker wirft den Patch also in die Menge (den Schwarm) und die Spieler organisieren sich untereinander diesen zu verteilen. Also läd man, bei diesem Vorgang, nicht vom offiziellen Server, sondern von Personen „wie dich und mich“ – jedoch natürlich nur von den Beteiligten.

    Nun zurück zu dem besorgten Spieler. Grundsätzlich handelt es sich hierbei auch um Programmaktualisierungen. D.h. der Programmcode wird entweder ersetzt oder Neuer wird eingefügt – je nach Updatestrategie. Ein Beweis hierfür ist auch leicht erbracht: Updater sind immer „extra“ Programme, also kein Unterprozess. So findet sich in dem entsprechenden Spielordner stets das Spiel selbst, als auch ein Updater als ausführbare (exe) Datei.

    Und daher nun endlich die Frage: Können mir andere Spieler „Schadcode“ übergeben, der sich dann, durch den Updatevorgang, auf meinem Rechner befindet?

    Damit habe ich mich etwas Näher befasst. Zunächst muss natürlich klar sein, dass diese Frage nicht für alle Spiele geklärt werden kann. Grundsätzlich werden Daten von unbekannten Quellen geladen und diese können durchaus Fehlerhaft sein – gewollt oder ungewollt. Das ist die schlechte Nachricht. Die Gute ist, dass sich viele Spielebetreiber Techniken bedienen, die sich mittlerweile als Standard etabliert haben. Das relativ bekannte „BitTorrent“ Protokoll ist eines dieser – wofür es auch sehr viele und gute Clients gibt. Bei dieser Technik erhält der Client ein File genannt „Torrentfile“. Dieses enthält eine Auflistung der Dateien, die geladen und verteilt werden müssen – zusätzlich weitere triviale Informationen.
    Am Ende, das lässt uns wieder aufatmen, ein SHA-1 Hash für jeden Part. Wer mag, kann an dieser Stelle einen Exkurs zum aktuellen Stand der Technik bzgl. der Sicherheit des SHA-1 unternehmen.

    ~

    Wieder zurück? Gut. Denn selbst wenn wir ein Programm hätten, das uns „günstig“ Kollisionen des SHA1 aufzeigt, wäre es sehr unwahrscheinlich, dass dabei ein Teil eines ausfühbaren Programmes herauskommt und gleichzeitig auch den gewollten Schadcode enthält. Diese Thematik lässt sicherlich Platz für Diskussionen – allerdings kann an dieser Stelle und an diesem Tag festgehalten werden, dass der SHA-1 Hashalgorithmus für diesen Einsatzzweck noch völlig genügt. Was ein Hashcode „genau“ ist, habe ich in diesem Beitrag beschrieben: http://cryptblog.de/2008/06/18/hacken-fur-anfanger/

    Es besteht also keinen Anlass zur Beunruhigung. Sofern der Tracker das Torrentfile korrekt an den Benutzer überträgt, ist ein P2P System (basierend auf BitTorrent), für diesen Einsatzzweck ausreichend sicher.

  • Mathematik zum Anfassen – Kryptographie

    Hallo!

    Diesmal nur ganz kurz eine kleine und Interessante Einführung in die Kryptographie, aus der Reihe „Mathematik zum Anfassen“ von Prof. Albrecht Beutelspacher:
    -> Video <-

    Einges davon sollte dem treuen cryptblog.de Fan schon bekannt sein.

  • Zufällige Entscheidungen

    Hallo zusammen,

    vor kurzem hatten ein Kommilitone und ich ein Problem. Wir wollten (über das Internet) ausknobeln, wer von uns mit dem Auto fahren muss und wer dafür Alkohol trinken kann. Ein Schnick-Schnack-Schnuck über das Internet sozusagen. Beide hatten wir nach einer Lösung für dieses Problem gesucht jedoch keine wirklich gute gefunden. Zuletzt entschieden wir uns dazu, es über die Anzahl der Heise.de-News des nächsten Tages zu bestimmen. Je nachdem ob es eine gerade oder ungerade Anzahl ist, muss der eine oder der andere.

    Die Frage ist also, ob es dafür bessere Lösungen gibt. Mit Hilfe einer dritten, unabhängigen Instanz sollte dies nicht so schwierig sein, einige Lösungsbeispiele habe ich dafür mal ausgearbeitet:

    Beide Parteien könnten mit einem Client auf einen Server verbinden. Sobald alle verbunden sind, gibt dieser eine zufällige Zahl aus. So hat man, synchronisiert, allen Teilnehmern dieses Ereignis zugänglich gemacht.

    Oder man könnte eine Webseite bereitstellen, die alle 5 Minuten eine zufällige Zahl ausgibt. So könnten beide Parteien Vermutungen über die nächste Ausgabe treffen und diesbezüglich eine Entscheidung finden. Um dieses Beispiel zu verdeutlichen habe ich diese Webseite angefertigt: http://www.cryptblog.de/random.php.

    Eine weitere Möglichkeit wären Kryptogramme eines Servers: Partei A bezieht ein aktuelles Kryptogramm von einem Server, welches eine verschlüsselte Zahl enthält. Er übergibt das Kryptogramm der Partei B und beide einigen sich darauf, welche Entscheidung bei einer geraden/ungeraden getroffen wird. Die Entschlüsselung ist allerdings erst später (~5 Minuten) möglich. Ich denke allerdings, dass diese Lösung unnötig kompliziert ist und kaum einen Vorteil gegenüber den anderen besitzt.

    Aber nun die Frage: ist es möglich eine solche Entscheidung zu treffen, ohne dass ein Dritter (Server) beteiligt ist? Meine Antwort darauf ist JA. Folgendes Verfahren habe ich mir überlegt:

    Sowohl A, als auch B, denken sich eine möglichst große zufällige Zahl (a und b) aus. Mit Hilfe einer Webseite, die hier lediglich als „Taschenrechner“ dient, berechnen A und B jeweils einen Hash (Fingerabdruck, beispielsweise MD5) ihrer Zahl, also z.B. H(a) und H(b). Über ein beliebiges Kommunikationsmedium kann nun dieser Hashwert ausgetauscht werden. Außerdem müssen sich A und B jeweils für eine gerade oder ungerade Zahl entscheiden. Durch diesen Austausch, haben sich beide auch damit einverstanden erklärt, dieses Verfahren zu nutzen. Nachdem also Hashwerte ausgetauscht sind, ist jeder im Besitz seiner eigenen Zahl und einem Fingerabdruck der Zahl des anderen.

    Jetzt kann jeder seine Zahl dem anderen nennen, ob nun A oder B zuerst ist egal. Beide Zahlen werden miteinander addiert, also m = a + b berechnet, und je nachdem ob diese Zahl gerade oder ungerade ist, fällt die Entscheidung für A oder B aus. Aufgrund des vorherigen Austausch der Hashwerte, ist ein nachträgliches ändern der Zahl nicht möglich bzw. A und B können die Aussagen des anderen verifizieren.

    Um dieses Beispiel zu verdeutlichen, existiert eine neue Sektion und ein Script um die Durchführung zu vereinfachen: http://cryptblog.de/muenzwurf/.

    Nochmal grob zusammengefasst:

    zufallprotokoll
    A prüft H(b)=H(b‘), B prüft H(a)=H(a‘). Sofern beides wahr, kann von a’=a und b’=b ausgegangen werden.
    Beide berechnen m = a+b.

    Mittels diesem Protokoll hat jeder Teilnehmer eine 50% Chance zu gewinnen:

    geradeungerade

    In der Anwendung ist folgendes zu beachten:

    Die Hashfunktion sollte einigermaßen sicher sein und um Rainbowtables entgegenzuwirken, sollten die Zahlen möglichst groß sein. Sofern dies erfüllt ist, können auch JavaScript Lösungen zum berechnen verwendet werden, wie z.B. http://aktuell.de.selfhtml.org/artikel/javascript/md5/ .

    Nachtrag:
    Grundsätzlich kann man dieses System auch, leicht modifiziert, für das bekannte Stein-Schere-Papier einsetzen, indem ein Hash von Stein|Zufallszahl, Schere|Zufallszahl oder Papier|Zufallszahl gebildet und später ausgetauscht wird. Das macht die vorherige Absprache ob gerade oder ungerade unnötig.

  • ITS-Quiz für Zwischendurch

    Hallo,

    es handelt es sich um Protokollsicherheit in Verbindung mit asymmetrischer Verschlüsselung. In diesem Szenario möchte die Partei A eine geheime Information an Partei B senden. A besitzt den geheimen Schlüssel zum öffentlichen Schlüssel PK_A, und B äquivalent PK_B. Hierbei wird folgendes Protokoll verwendet:

    (1) A –> B:     (A, E(PK_B, A|M), B)
    (2) B –> A:     (B, E(PK_A, A|M), A)

    also: (Absender, Nachricht, Empfänger) wobei Nachricht = Absender|Information.

    Schritt für Schritt: A sendet an B eine Nachricht, diese besteht aus

    • dem Absender (A),
    • dem asymmetrisch verschlüsselten Text M wobei dieser noch mit  und dem Absender verbunden wurde (A|M),
    • dem Empfänger (B).

    daraufhin bestätigt B den Erhalt der Nachricht durch:

    • den Empfänger (B),
    • die exakt identische Nachricht, diesmal allerdings mit dem öffentlichen Schlüssel des ursprünglichen Absenders – also des neuen Empfängers (PK_A) verschlüsselt,
    • den Absender der usprünglichen Nachricht (A).

    E(PK_X, M) ist die asymmetrische Verschlüsselung, z.B. RSA, mit Hilfe des öffentlichen Schlüssels X, im obrigen Beispiel also jeweils des Empfängers. Das Ganze etwas anders ausgedrückt: Die Partei A sendet eine Nachricht an B, wobei diese mit dem öffentlichen Schlüssel des Empfängers verschlüsselt wurde und außerdem auch den Absender enthält.

    Im Zuge einer Umstellung wurde das Protokoll abgeändert auf:

    A –> B:     (A, E(PK_B, M), B)
    B –> A:     (B, E(PK_A, M), A)  (Bestätigung)

    Der Unterschied: der Absender ist hier nun nicht mehr innerhalb der verschlüsselten Nachricht enthalten.

    Frage: ergibt sich daraus ein Problem? Wo ist der Unterschied bzw. gibt es überhaupt einen?

  • Auflösung Februar

    Hallo liebe Gemeinde,

    eine Vermutung wurde ja geäußert (siehe Kommentare). Dieser geht in die Richtung, den Klartext mit einem zufälligen Schlüssel zu chiffrieren und diesen wiederrum mit dem geheimen (ausgetauschten) zu verschlüsseln und an die Nachricht anzuhängen. Also: [E_tempkey(Text) | E_key(tempkey)]. Also ein ähnliches System wie bei den DLC-Containern.

    Die Idee ist natürlich nicht schlecht, allerdings handelt es sich hierbei um etwas anderes. Und zwar gibt es in der Praxis verschiedene Betriebsmodi; um einige zu nennen: ECB, OFB, CFB. Und an dieser Stelle wurde der CBC „Cipher Block Chaining“ Modus verwendet. Was dies nun genau bedeutet ist etwas schwierig zu eklären, daher beschränke ich mich an dieser Stelle darauf den Unterschied zwischen dem simpelsten (ECB) darzustellen.

    Beim ECB-Modus wird der Klartext in gleiche Stücke getrennt. Im Beitrag zur Bildverschlüsselung (http://cryptblog.de/2008/10/06/bildverschlusselung/) hatte ich dieses Verfahren bereits erläutert. Dort wurde

    “Hallo, wie geht es dir  ”

    in:

    “Hallo, w”, “ie geht “, “es dir  ”

    aufgeteilt. Jeder dieser Blöcke wird mit dem gleichen Key verschlüsselt und so erhalten wir am Ende wieder 3 Blöcke. Beispielhaft dargestellt:

    “mdjwbcxg”, “ötüeoejd”, “ndkrdkdp”.

    Angenommen ich ändere das „Hallo“ im Klartext in ein „Hello“, so würde sich nur der erste Block ändern, die anderen zwei blieben unberührt. Und um diesen Einfluss zu vergrößern gibt es die oben genannten Betriebsmodi. Ein Bild dazu aus Wikipedia zum CBC-Modus:

     cbc_encryption

    Zunächst schwierig zu verstehen. Auf der linken Seite haben wir den sehr bekannten Initialisierungsvektor. Bei der Blowfish-Implementierung wird dieser einfach zufällig gewählt. Er wird mit dem Klartext verrechnet (XOR). Das Ergebnis daraus, wird verschlüsselt und ergibt den Chiffretext welches wiederrum auf den nächsten Klartextblock Einfluss nimmt. Durch diese Pfeile ist also zu sehen, dass der Vorgänger immer auf den unmittelbaren Nachfolger einwirkt.

    Dadurch ergibt sich eine Kette: wird am Anfang eine Veränderung vorgenommen, ändert dies den kompletten restlichen Chiffretext. Und da, wie schon erwähnt, der IV gewürfelt wird, ergibt sich bei jeder Verschlüsselung einen anderen Chiffretext. Zur Entschlüsselung wird allerdings dieser Vektor benötigt, daher wird er einfach mitgeschickt. Aus dem Plaintext P wird also nicht nur ein Chiffretext C, sondern beinhaltet auch einen IV.

    Verstanden sollte sein, dass diese „Block für Block“-Verschlüsselung Probleme bereiten kann und ein Betriebsmodus, wie der CBC, für noch mehr Einflussnahme des Klartextes sorgt.

  • Frage des Monats (Februar)

    Nicht grade traditionsgemäß, aber um mal Abwechslung in den Cryptblog Alltag zu bringen.

    Wir betrachten folgende Internetseite:
    http://www.php-einfach.de/sonstiges_generator_blowfish_js.php

    Der angezeigte Key wird zufällig ausgewürfelt und kann ähnlich wie der Klartext geändert werden, muss aber nicht. Danach besteht die Möglichkeit, die Eingabe zu verschlüsseln, worauf eine Ausgabe des verschlüsselten Textes im Base64 erfolgt. Mal als Eingabebeispiel:

    Key: tsu15bdi
    Klartext: test

    Und nun? Jetzt kann mit dem „Verschlüsseln“-Button chiffriert werden. Um dies hier alles nachvollziehen zu können, sollte dies nun jeder einmal durchführen. Nun kommt das große „Problem“. Mit den oben genannten Daten ergibt sich:

    AAtRZQALh6Bkp67o8pNUbg==

    Wenn ich aber mehrmals den Button betätige, entsteht immer wieder etwas anderes:

    AAUYzgALLpTtP2+zdG0O4A==
    AAD+sgAJaAF/3D3mdFxHWw==
    AA874gALmyCaU23yyjVKcQ==
    AAHn2gAKE4mfFu4zg/muTQ==

    Und es handelt sich dort jeweils um „test“. Jeder dieser Ergebnisse kann mit dem oben genannten Passwort auch wieder nach „test“ dechiffriert werden. Genaugenommen zu

    „test    „

    was 8 Zeichen mit jeweils 16 Bit = 128 Bit (Blockgröße) entspricht, dies allerdings nur am Rande.

    Normalerweise geht man davon aus, das ein fester Klartext P mit dem festen Schlüssel K nur EIN eindeutiges Ergebnis zurückliefert, um das Entschlüsseln bzw. die Umkehrbarkeit eben möglich ist. Bei der einfachen (additiven) Cäsar Verschiebechiffre ist das ja ähnlich (Schlüssel 2):

    A -> C
    B -> D
    C -> E

    etc.

    Das oben gezeigte verhält sich also so, als würde A (nach Verschlüsselung) sowohl zu C als auch zu D und E verschlüsselt werden. Und dies jeweils zufällig.

    Frage: Wieso ist hier eine eindeutige Entschlüsselung möglich?