Hallo zusammen,
heute möchte ich präsentieren, welche „Alltagsprobleme“ sich in der Kryptologie wiederfinden.
Vor kurzem hat mich jemand angeschrieben, er säße vor einem kleinen mathematischen Problem. In seinem Dorf ist ein so genanntes Kuhfladen-Bingo geplant. Dafür muss ein Feld von fester Größe, in eine dynamische Anzahl kleinerer unterteilt werden. Nochmal langsam:
Wir haben zunächst das große Feld bzw. die Wiese. Diese hat eine konstante Größe bzw. im Falle, dass sie rechteckig ist, eine Länge und eine Breite. Jetzt haben wir x Lose verkauft und wollen dieses Feld in x-viele gleichgroße „kleine“ Felder aufteilen. Die Summe aller kleinen Flächen entspricht der Gesamtgröße – also wir wollen stets einen Gewinner und keine „unbesetzten“ Felder. Es soll also ein Schachbrettmuster auf dieses Feld gelegt werden, wobei in diesem Fall die kleinen Felder nicht quadratisch sein müssen.
Mathematisch ausgedrückt, suchen wir zwei ganzzahlige n und m, wobei n*m = x und x die Anzahl der verkauften Lose ist. Kennen wir n und m, können wir die Länge bzw. Breites des Feldes durch n bzw. m teilen und erhalten die Größe der „kleinen“ Rechtecke. Ein Beispiel:
Das Feld ist L=8 x B=16 Meter groß. Es wurden zufällig 1024 Lose verkauft. Also suchen wir:
n * m = 1024
Eine Lösung ist: n = 4, m=256. Demnach teilen wir die Länge L=8m durch 4 und erhalten l=2m – außerdem die Breite B=16m durch 256 und erhalten b=0,0625m. Ein kleines Feld hat also die Ausmaße l=4m und b=6,25cm. Wie wir allerdings schnell erkennen, gibt es bei dieser Gleichung mehrere Lösungen. Ebenso wären n=8, m=128 und sogar die triviale Lösung n=1 und m=1024 in der Lösungsmenge enthalten.
Einen naiven Lösungsalgorithmus finden wir also schnell: wir suchen einen Teiler von x im Intervall [2, sqrt(x)] also zwischen 2 und der Wurzel von x. Bei x=1024 ist das die 2, die 4, die 8, die 16 und die 32. Das lässt sich relativ einfach mit einer Schleife realisieren.
Daraufhin ergab sich die Frage, ob dafür nicht auch eine bessere bzw. effizientere Lösung existiert. Das Beste wäre eine Formel, in welcher nur die Variablen einzutragen sind und dann ein brauchbares (nichttriviales) Ergebnis präsentiert. An dieser Stelle möchte ich dem Leser Zeit geben um darüber nachzudenken. Auch bezüglich der Frage, warum sich dieses Problem in einem Blog über Kryptologie wiederfindet.
~
Ich habe eben gezeigt, dass wir bei diesem Problem zwei ganzzahlige Teiler suchen: n und m bzw. n*m=x. Ich ändere nun mal die Namen der Variablen: p*q=m. Sei also m ein RSA-Modul, also das Produkt zweier Primzahlen, so sind p und q ganzzahlige Teiler von m. Wir haben also „mehr oder weniger“ nach einem effizienten Algorithmus bzw. einer Formel gesucht, die RSA-Verschlüsselung zu brechen. Wären wir an jenem Abend erfolgreich gewesen, würde ich diesen Blogeintrag an einem Strand in der Karibik zu Ende schreiben.
Wie schon oft erwähnt, ist die „schwierige“ Suche nach den Primzahlen p und q genau das, was die RSA-Verschlüsselung ausmacht. Und die Tatsache, dass für p*q=m (p,q prim) bisher noch kein effizienter Algorithmus gefunden wurde, bietet uns Schutz bei Online Banking, Zertifikaten (PKI), VPN-Tunneln und vielem mehr.
Moooooooment. Da steht doch p*q=m (p,q prim) – also wir suchen zwei Primzahlen dessen Produkt m ergibt. Bei unserem Problem oben war jedoch die Rede von einem beliebigen Teiler! Stimmt. Es folgt ein Ausflug in die Zahlentheorie und theoretische Informatik.
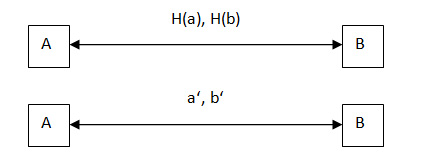
Angenommen wir hätten das oben beschriebene Feldaufteilungsproblem effizient gelöst, dann wären wir im Besitz einer Formel oder eines Algorithmus, den wir einfach F nennen – F für Feld. Wir übergeben dem Algorithmus F also die Anzahl der Lose und selbiges generiert uns zwei ganzzahlige Teiler n und m. Auf der anderen Seite haben wir das RSA-Problem – wir besitzen also einen „langsamen“ Algorithmus für dieses Problem und nennen diesen R. Wir übergeben R ein RSA-Modul (also das Produkt zweier Primzahlen) und es liefert uns das entsprechende p und q.
Damit sind F und R also informell definiert. Nun übergeben wir, nur aus Spaß, unserem Feldproblem F ein RSA-Modul, sagen wir r(=p*q). Warum auch nicht – es ist ja auch nur eine Zahl. F liefert uns nun also zwei ganzzahlige Teiler n und m wobei gilt: n*m=r. Jetzt wird’s spannend: nach dem Fundamentalsatz der Arithmetik ist die Primfaktorzerlegung eindeutig und stets existent. D.h. das, was wir hier zurückbekommen, müssen p und q sein. Warum? Angenommen es gäbe noch eine andere Aufteilung z.B. a*b=r, dann hätte sowohl a, als auch b eine Primfaktorzerlegung (Existenz!) welche nicht mit p*q übereinstimmt. Das ist ein Widerspruch zur Eindeutigkeit – somit haben wir indirekt p=n und m=q bewiesen. #
Dieser Teil muss nun nicht unbedingt verstanden worden sein. Wichtig ist nur, dass wir das Problem R, also die Zerlegung eines RSA-Moduls, mit Hilfe von F lösen können. In der Informatik spricht man hier auch von Turingreduzierbarkeit. Wenn wir wissen, dass wir R mittels F lösen können, dann muss R „leichter“ sein als F, bzw. „R ist turingreduzierbar auf F“ oder „F ist Orakel für R“. So lassen sich Probleme in Klassen einteilen, was relativ komfortabel ist: sobald wir einen guten Algorithmus für F gefunden haben, ist auch effizient R gelöst. So müssen wir also nur nach einer Lösung für F suchen, wobei diese auch schwieriger sein könnte als R. Äquivalenz liegt vor, wenn eine Reduktion in beiden Richtungen möglich ist. Um die Frage vorweg zu nehmen: dies ist hier der Fall; F und R sind Turing-Äquivalent (ohne Beweis).
So sind wir von den Kühen, über die Kryptologie, zur theoretischen Informatik gekommen.