———————————————————————–
Hier geht es zum Münzwurf
———————————————————————–
Erklärung
Hier wurde das Problem behandelt, zwischen zwei Gesprächspartnern eine zufällige Entscheidung (Münzwurf) zu finden, ohne dass dabei die Nutzung einer weiteren unabhängigen Instanz notwendig wird.
Folgende Ziele müssen dabei berücksichtigt werden:
- der Teilnehmer muss das Ergebnis aktiv beeinflussen können,
- beide Teilnehmer müssen zu dem gleichen Ergebnis gelangen,
- eine Manipulation durch einen Teilnehmer darf nicht möglich sein,
- das Verfahren muss offen und deterministisch sein.
Zunächst soll das System beschrieben werden um dann die Erfüllung dieser Punkte zu belegen.
Im ersten Schritt kann jede Partei (A oder B) eine zufällige, jedoch veränderliche Zahl festlegen, welche zunächst als geheim zu betrachten ist. Mittels einer Einwegfunktion (Hashfunktion), in diesem Fall MD5, wird daraus ein Fingerabdruck erstellt. Hier besteht die Einschränkung, dass die ausgewählte Zahl möglichst groß ist um Angriffe mittels Tabellen (Rainbowtable) entgegenzuwirken. Der Zufallsgenerator generiert nur Zahlen dessen Länge größer 10 ist. Im nächsten Schritt können beide Parteien die ermittelten Hashwerte austauschen. Durch den Austausch stimmen auch beide Seiten konkludent der Verwendung dieser Anwendung zu. Jede Seite besitzt also nun die eigene geheime Zahl und einen Fingerabdruck der Gegenseite. Vor oder nach diesem Austausch muss allerdings noch festgelegt werden, welche Gewinnsituation nach welcher Entscheidung (gerade / ungerade) vorliegt. Nachdem Einigung herrscht, können die gewählten, bisher geheimen, Zahlen nun ohne bedenken ausgetauscht werden.
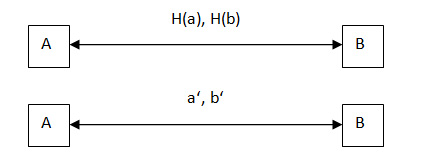
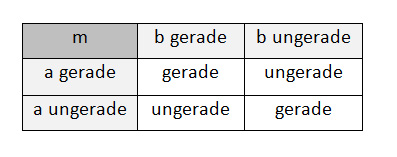
Das System berechnet m = a + b, wobei a das Geheimnis von A und b das Geheimnis von B ist. Es besteht hierbei eine 50% Chance, dass m gerade oder ungerade ist. Durch die zuvor gewählte Zahl ist das m und dessen Eigenschaften beeinflussbar, wodurch (1) erfüllt ist.
Ein nachträgliches Ändern der gewählten Zahl, würde einen fehlerhaften Hashwertabgleich ergeben. Es muss H(a) = H(a‘) und H(b) = H(b‘) gelten. Daher ist eine Manipulation durch eine Seite ausgeschlossen (3). Da am Ende beiden Seiten sowohl a als auch b bekannt ist, wird auch das gleiche m berechnet, zumal die Addition kommutativ ist (2). Zuletzt ist also zu prüfen ob das Verfahren offen und deterministisch ist. Bei der verwendeten Hashfunktion handelt es sich um den Message Digest 5 Algorithmus, welcher schon in zahlreichen Anwendungen verwendet wird. Ein beliebiges x führt auch stets zu dem gleichen f(x) – es gibt keine weiteren Einflussfaktoren. In diesem Fall wurde die Clientseitige Programmiersprache JavaScript verwendet, d.h. alle Berechnungen finden auf dem Rechner des Benutzers statt. Eine Verbindung zum Server besteht nach vollständigem Laden der Webseite nicht. Rein theoretisch wäre ein Berechnen „von Hand“ möglich, die Webseite dient hier also lediglich als Taschenrechner.
Damit sind alle Forderungen erfüllt. Solange der MD5 innerhalb dieses Zahlenraums vertretbar (in Bezug auf diese Anwendung) sicher bleibt, gilt dies auch für dieses Verfahren.