Zur Abwechslung mal wieder etwas aus der Praxis. Heute geht es um die mittlerweile verbreiteten DLC-Container. Für die Leute, die damit nichts anfangen können, zunächst eine Zusammenfassung.

Dieses System wurde entwickelt, um Links zu verschlüsseln bzw zu verdecken. Die Benutzer sollen fähig sein, Daten von Servern herunter zu laden, ohne sehen zu können wo diese nun genau liegen. Also eine Containerdatei die Text (Linklisten) enthält, aber nicht von dem Benutzer – zumindest nicht auf einfache Art und Weise – eingesehen werden soll. Der Sinn bzw. Zeck kann von jedem selbst nachgeforscht werden.

Etwas nicht sehen dürfen? Also eine Verschlüsselung. Die Frage ist allerdings, wie hält man etwas vor dem Benutzer geheim, welcher den Inhalt allerdings selbst benötigt. Kurz gesagt: das geht natürlich in der elektronischen Welt nicht. Es ist z.B. durch einen modifizierten Proxy oder das Mitschneiden des Netzwerkverkehrs trotzdem möglich die Links zu erhalten. Die Frage, die allerdings nun hier beantwortet werden soll: „ergibt das Ganze dann noch Sinn?“. Und die Antwort darauf ist erstaunlicherweise: Ja.

Zunächst wollen wir uns Schritt für Schritt dem System nähern. An dieser Stelle muss ich sagen, das obwohl dieses eigentlich Open Source und „Dokumentiert“ ist, es keine wirklich brauchbaren Informationen darüber gibt wie es umgesetzt wurde. Wahrscheinlich um zu verhindern das jemand Schwachstellen findet, wie es bei ähnlichen Systemen geschehen ist. So musste ich ziemlich alles selbst erarbeiten, allerdings denke ich, das meine Argumentation schlüssig ist.

Zuerst war das Wort.. oder die Datei. In diesem Fall der DLC-Container, welchen ich über ein Webinterface der Herstellerseite erstellt habe. Im Cryptool betrachte ich den Inhalt:

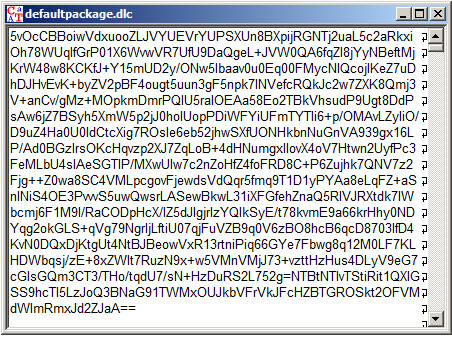
Nun, dies ist offensichtlich kodiert. Ja – kodiert und nein, das ist (bisher) keine Verschlüsselung. Es handelt sich um die Base64 Kodierung, welche häufig in Protokollen oder beim Übertragen chiffrierter Daten verwendet wird. Informationen darüber finden sich an jeder Ecke; an dieser Stelle genügt es zu sagen, das wir diese verlustfrei dekodieren können:

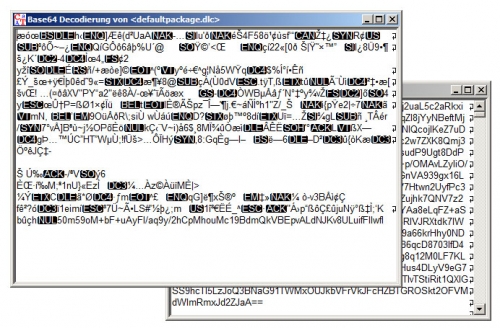
Auf den ersten Blick sieht es tatsächlich so aus, als ob es uns nichts Neues gebracht hätte.  Dann betrachten wir das Ende dieser Datei etwas genauer:

Was ist hier zu sehen? Zunächst unlesbarer Text bei welchem es sich offensichtlich um verschlüsselten Inhalt handelt, dann ein Nullbyte (0000 0000), und dann, sehr unerwartet, erneut ein Base64. Dieser kann nun erneut dekodiert werden, wobei sich daraus (ähnlich wie oben) lediglich unlesbarer Inhalt ergibt.

Was ist das alles nun? Naja, im oberen Teil befinden sich offensichtlich die Hauptinformationen. Wie eine Signatur liegt dort nun eingebettet eine Zeichenkette, die Besonders zu sein scheint. Nun ist die Frage was man damit machen kann. Zuerst war die Vermutung das es sich dabei um ein asymmetrisch verschlüsseltes Passwort handelt. Allerdings müssten dann die Informationen zum dechiffrieren hartkodiert im Quelltext vorliegen womit das System (insbesondere bei einer Java Anwendung) sehr schnell geknackt wäre.

Nach längerem überlegen kam ich zu dem Entschluss, das es also nur 2 Möglichkeiten gibt: die Sache ist einfach nur sehr oberflächlich und daher „simpel“, oder wirklich clever. Vorweg, ich musste erfahren das letzteres zutrifft.

Um diesem Problem nun gegenüber zu treten, habe ich den verursachten Traffic der Anwendung mitgeschnitten: also mir angeschaut was das Programm von meinem Computer aus ins Internet sendet. Und siehe da, dort war die Lösung. Und zwar gibt es beim Verarbeiten der DLC-Datei einen Datenaustausch zwischen einem Server und der Anwendung. Zuerst schickt das Programm eine Anfrage an den Server, welcher wiederrum antwortet. Und was dort uA gesendet wird ist hier zu sehen:

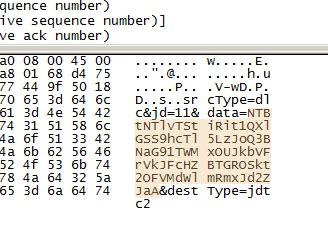
Erneut wird im Base64 eine Zeichenkette über den Äther geschickt. An dieser Stelle war ich der Verzweiflung nahe, da es sich hierbei erneut um einen String handelt, den ich vorher noch nicht gesehen hatte. Wieder stand ich vor einem Problem, dessen Lösung allerdings recht einfach war:

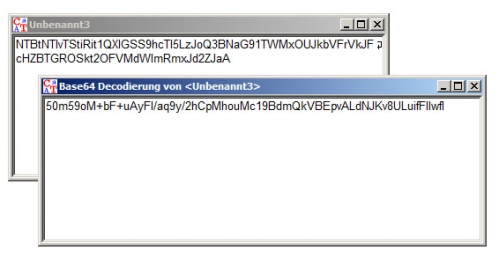
Und zwar ist das die Base64 Zeichenkette aus der DLC-Datei, erneut in einen Base64 eingepackt. Dies ergibt eigentlich keinen Sinn und scheint eher ein „Fehler“ zu sein bzw. Faulheit der Programmierer. Egal, es ist nun nachgewiesen das diese „besondere“ Signatur zum Server gesendet wird. Nach dieser Anfrage, antwortet der Server mit einer Base64 Zeichenkette (FVZ+8D1u+4Tey+5pSkwNP+SgUTaGXGlRt8kMywjdEkM=), die ich schonmal für uns im Cryptool ausgepackt habe:

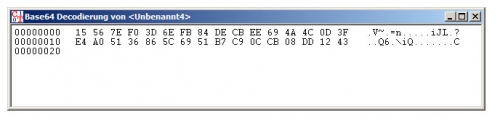
Damit ist der Beweis erbracht. In der Datei ist eine Zeichkette enthalten, die nur vom Server entschlüsselt werden kann und das Passwort enthält, mit welchem die Datei vom Programm nutzbar gemacht werden kann. Wieso? Nunja, wir betrachten das letzte Bild, also die Antwort vom Server nach unserer Anfrage. Es handelt sich dabei um ganz exakt 256 Bit. Die typische Länge für z.B. einen AES256. Es kann an dieser Stelle kein asymmetrischen Verfahren verwendet worden sein, da dieses niemals unter 1024 Bit lang wäre. Es ist also sehr wahrscheinlich das hier der Schlüssel dirkt oder zumindest teilweise enthalten ist.

Nach dem was hier zu sehen war, funktioniert das System meiner Meinung nach so: möchte der Benutzer eine DLC-Datei auswerten, läd er diese in das entsprechende Programm. Da der Inhalt verschlüsselt ist, kann die Anwendung damit zunächst nichts anfangen. Innerhalb der Datei befindet sich allerdings das (verschlüsselte) Passwort zum entschlüsseln der Daten, welches jedoch nur vom Betreiber entschlüsselt werden kann. Die Applikation sendet also dieses verschlüsselte Passwort zum DLC-Server, welches die entschlüsselte Version zurückliefert. Damit kann der Inhalt dechiffriert werden kann. Nochmal zusammengefasst:

1. das Öffnen der DLC-Datei mit dem Programm,
2. die Anwendung sendet das verschlüsselte Passwort zum Server des Betreibers,
3. der Betreiber dechiffriert dieses und sendet das entschlüsselte Passwort zurück,
4. mit diesem Passwort kann der Inhalt dechiffriert werden und die Links „liegen offen“.

Wofür das Ganze? Der Betreiber kann auf diese Art und Weise kontrollieren, wer (von welcher IP-Adresse) wie häufig eine Datei entschlüsseln möchte. Der Sinn ist zu verhindern, das jemand große Mengen dieser Container entschlüsselt und damit die Links alle freilegt. Ohne Zusammenarbeit mit dem Server ist das entschlüsseln dieser Dateien bzw.der dort enthaltenen Links nicht möglich.

Insgesamt halte ich dieses System für ganz gelungen. Unter Umständen werde ich in einem separaten Eintrag noch einige Anmerkungen dazu machen.

Nachdem ich nun in den letzten Wochen Staffelweise 24 geschaut habe, will ich einige Aussagen (die ich so gehört habe) kommentieren.

„das ist Blowfish verschlüsselt, das erkennt man am Header.“

Klingt gut, ist aber Unsinn. Eine verschlüsselte Datei bzw. ein verschlüsselter Container besitzt keinen besonderen Header. Natürlich könnte man dem zurecht entgegenhalten das dies Anwendungsspezifisch ist. Jedoch wo liegt der Sinn einem Angreifer schon vor Eingabe des Passworts den Algorithmus zu verraten (lassen wir Kerkhoff außen vor).  Sofern kein besonderer Verschlüsselungsalgorithmus ausgewählt ist, führen Programme „Probeentschlüsselungen“ durch und prüfen auf Plausibilität. 

Decryption is considered successful if the first 4 bytes of the decrypted data contain the ASCII string “TRUE“, and if the CRC-32 checksum of the last 256 bytes of the decrypted data (volume header) matches the value located at byte #8 of the decrypted data (this value is unknown to an adversary because it is encrypted – see the section Header Key Derivation, Salt, and Iteration Count). If these conditions are not met, the process continues from (3) again, but this time, instead of the data read in (1), the data read in (2) are used (i.e., possible hidden volume header). If the conditions are not met again, mounting is terminated (wrong password, corrupted volume, or not a TrueCrypt volume).

Quelle: http://www.truecrypt.org/docs/encryption-scheme.php

Außerdem ist Blowfish (128 Bit) schwer veraltet.

Definieren wir das Ganze einfach mal als zweifelhaft.

Als nächstes:

„das ist eine affine Chiffre, die kann man nicht knacken“

Okay, Blowfish geht, aber eine (linear) affine Chiffre nicht. Die Affine Chiffre ist (das findet auch jeder in Google) eine einfache Blockchiffre, welche allerdings im Gegensatz zur einfachen Verschiebechiffre noch einen 2. Schlüssel hat. Der Schlüssel ist also ein zwei-Tupel: k=(a,b). Wenn wir eine Alphabetsgröße von 26 festlegen, verschlüsselt sich Text mit Hilfe folgender Formel:

c = a*p + b mod 26

Wobei c das neue Chiffre- und p ein Klartextzeichen ist. Ein Beispiel:

Klartext: „ABC“, Key: (2,3)

2 * 0 (A) + 3 mod 26 = 3 (C)
2 * 1 (B) + 3 mod 26 = 5 (E)
2 * 2 (C) + 3 mod 26 = 7 (G)

Chiffretext = „CEG“

Zum entschlüsseln muss ein mulitplikatives Inverses berechnet werden.

Das versteht man also unter einer affinen Chiffre. Natürlich ist etwas kniffeliger als eine reine Verschiebe oder Vignerechiffre, jedoch nicht wirklich ein Problem. Mit ein wenig Verstand bekommt man es auch noch gut auf dem Papier hin.
Diese Aussage können wir zweifelsfrei als Unsinn bezeichnen.

Dieses Thema ist mir persönlich sehr wichtig da darüber sehr viel Unwissen herrscht. Rein theoretisch könnten digitale Signaturen dafür sorgen, das unsere E-Mail Postfächer fast spamfrei bleiben. In der Praxis werden Sie jedoch leider (auch aus Kostengründen) nicht dafür verwendet. Dafür gibt es andere gute Anwendungsmöglichkeiten die ich auch präsentieren möchte.

Im ersten Teil jedoch, will ich eine kurze Einführung in die Technik „dahinter“ geben um im zweiten Teil das organisatorische, also PKI (Public-Key-Infrastruktur), zu erklären.

Wie funktionieren überhaupt diese digitalen Unterschriften? In der realen Welt stellen wir mit einer persönlichen Unterschrift Verbindlichkeit zwischen dem Text auf dem Papier und dessen Inhalt her. Wenn ich also etwas unterschreibe, nehme ich den Text (inhaltlich) zur Kenntnis. Dies hat auch eine gewisse Beweiskraft, da die Authentizität der Unterschrift geprüft werden kann.

Im Gegensatz zum realen Leben, lässt sich im Internet allerdings alles „kopieren“. Ich könnte eine Unterschrift also einfach irgendwo ausschneiden und unter einen anderen Text kleben. Ob das nun auch in der wirklichen Welt möglich ist lasse ich einfach mal offen. Sicher ist jedoch, das es auf dem Computer viel einfacher geht.

Also muss die digitale Unterschrift in Zusammenhang mit dem Text stehen, so das ein Verändern des Textes auch gleich die Unterschrift zerstört. Und genau so funktioniert das auch. Kommen wir also zu den Details.

Zunächst der Text:

Hiermit nehme ich Ihr Angebot auf Abschluss eines Kaufvertrags vom 25.06.2008 bzgl. drei Gläser Weizenbier schriftlich an.

Dies ist also der Text (z.B. in einer E-Mail) der zu unterschreiben ist. Der erste Schritt besteht nun darin, aus diesem Text ein Fingerabdruck zu erstellen. Wie wir bereits wissen, ist dies mit Hashfunktionen wie z.B. MD5 oder SHA möglich. Der Grund dafür ist eigentlich nur, die Länge der Signatur möglichst klein zu halten.

Hash(Text) = f998fb1e1a73549287404a43a2506801

Ich habe aus meinem Text also nun einen kompakten Hash (MD5) erstellt. Weiter geht es…

… und zwar mit dem RSA Verfahren. Ja, es taucht überall auf und das ist auch Grund warum dieses System so wichtig ist. Ich möchte nicht nochmal im Detail darauf eingehen wie damit ver- und entschlüsselt wird denn dies ist in den Grundlagen schon hinreichend beschrieben. Diese komplett im Detail zu verstanden haben ist allerdings auch nicht so unbedingt notwendig. Sehr wichtig dagegen ist folgendes:

Sei E( text ) die Funktion zum verschüsseln (RSA), sei D( text ) die Funktion zum entschüsseln (RSA), jeweils mit dem gleichen Schlüssel.

1) E ( Klartext ) = Chiffretext
2) D ( Chiffretext ) = Klartext
3) D ( E ( Klartext ) ) = Klartext
4) E ( D ( Klartext ) ) = Klartext

Zeile 1 und 2 sind denke ich recht offensichtlich. Ich verschlüssel einen Text und erhalte den verschlüsselten Chiffretext und umgekehrt. In Zeile 3 wird das beschrieben, was im Internet so geläufig ist: ich verschlüssel einen Text (mit E), sende ihn und erhalte (durch D) den Klartext zurück. Wichtig ist also die Zeile 4: wenn ich einen Text entschlüssel, also D anwende, erhalte ich auch eine Art von Chiffretext. Und wenn ich diesen entschlüsselten Text wieder verschlüssel, erhalte ich den Klartext.

Dieses Verfahren wird auch bei den digitalen Signaturen eingesetzt. Ich bilde (wie oben beschrieben) einen Hash aus dem Text und entschlüssel ihn mit meinem (geheimen) privaten Schlüssel. Niemandem (außer mir) ist der private Schlüssel bekannt und daher kann auch nur ich diese Signatur leisten. Der „entschlüsselte“ Text wird einfach an die E-Mail angehangen.

Die Validierung der Signatur ist jedem möglich, indem er den „entschlüsselten“ Text mit dem öffentlichen Schlüssel des E-Mail Absenders verschlüsselt. Dadurch erhält er den Hashcode und kann diesen abgleichen. Das ganze nochmal mit Beispiel:

Hash(Text) = f998fb1e1a73549287404a43a2506801

hatten wir eben ausgerechnet. Nun wird der Hashcode mit dem privaten Schlüssel entschlüsselt.

DECRYPT ( privatekey , „f998fb1e1a73549287404a43a2506801“ )
= dfmkomogerglmmerfohgnjutrihdmfkosemvgtjngrmakofrjlsgnhbhrgnamghktmhkke
(nur Beispielhaft)

Dieser wird an die E-Mail einfach angehangen

Hiermit nehme ich Ihr Angebot auf Abschluss eines Kaufvertrags vom 25.06.2008 bzgl. drei Gläser Weizenbier schriftlich an.
dfmkomogerglmmerfohgnjutrihdmfkosemvgtjngrmakofrjlsgnhbhrgnamghktmhkke

Die E-Mail wird versendet. Die andere Seite verwendet den öffentlichen (allen bekannt da veröffentlicht) des Absenders und verschlüsselt

ENCRYPT ( publickey , „dfmkomogerglmmerfohgnjutrihdmfkosemvgtjngrmakofrjlsgnhbhrgnamghktmhkke“)
= f998fb1e1a73549287404a43a2506801

Nun bildet der Empfänger einfach den Hashcode vom Text und gleicht die 2 Werte ab:

Hash(Text) =?= f998fb1e1a73549287404a43a2506801

Wenn beide Werte identisch sind, ist die Signatur gültig.

Angenommen ein böser Mensch würde nun den Inhalt ändern wollen, also folgende Änderung durchführen:

Hiermit nehme ich Ihr Angebot auf Abschluss eines Kaufvertrags vom 25.06.2008 bzgl. zehn Gläser Weizenbier schriftlich an.

würde sich folgender neuer Hashwert ergeben:

Hash(neuerText) = cc8bfa6863caafd65d3476c390ece04a 

und der Abgleich mit der Signatur (f998fb1e1a73549287404a43a2506801) schlägt fehl.

Die Funktionsweise sollte damit klar sein. Irgendwie muss jedoch auch beweisbar sein, das die Unterschrift auch wirklich von DIESER Person kommt und nicht von einer anderen… (Cliffhanger)